内聚力单元在集成电路后端结构界面模拟中的应用

与断裂力学理论对比，内聚区建模是Dugdale^[19]和Barenblatt^[20]开创性思维的结果，这种建模方法不需要给定初始裂纹。而且，这种方法可以用来描述断裂的初始状态和生长过程。最后，因为它既可用于研究脆性失效的特性，又能用于研究韧性失效的特性，所以它是一种通用方法。

内聚区建模的基本思想是，在裂纹尖端附近将裂纹分为无应力区域和应力区域，在应力区域加载所谓的内聚力，因而在裂纹尖端处就不存在无限大的应力。断裂被视作一个渐进的过程，在此过程中材料的失效发生在裂纹尖端的扩展区或内聚区，但是内聚力会阻碍断裂的发生^[21]。在有限元分析中，内聚区的单元通常是放置在连续单元之间，因此当考虑界面脱层问题时，这种方法非常具有吸引力^[21，22]。

内聚力可以通过所谓的“牵引力分离力定律”来计算，该定律描述了界面处分离力矢量δ与牵引力矢量t之间的关系（见图4.4）。

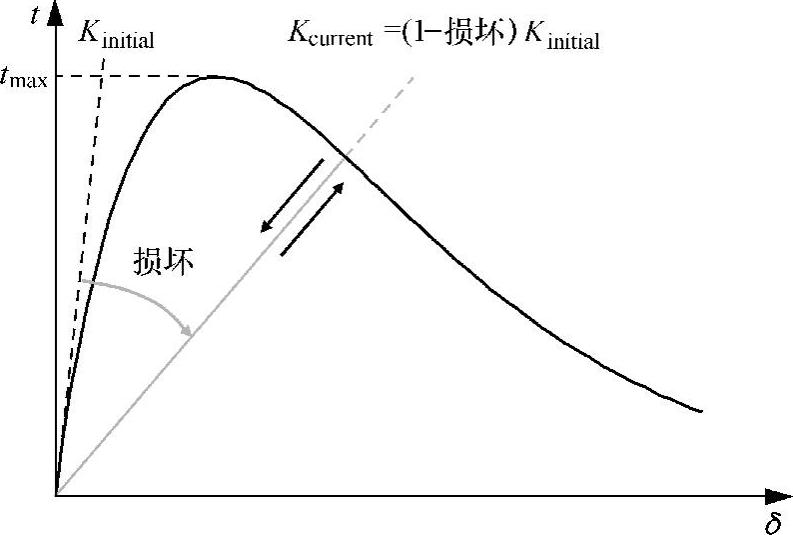
图4.4 典型的（指数型）牵引力分离力定律，当前的 硬度描述了加载时/卸载时的弹性特性

因此，依据Van Hal等人^[23]提出的方法，我们采用了Smith-Ferrante模型，且根据Ortiz和Pandolfi^[21]提出的研究框架，考虑了分离过程的不可逆性，得到的牵引力分离力定律如下：

式中，t为等效牵引力；δ_c为最大牵引力t_max对应的有效位移；δ为有效分离力，其定义如下：

式中，本构参数β定义为临界剪切力与临界正牵引力的比值。式（4.7）中的尖括号的定义是<x>＝0.5（x+x），只有正的法向分离力才会影响有效分离力。有效分离力的功如下^[21]：

(www.xing528.com)

商业的非线性有限元软件MSC.Marc已经将内聚区单元作为用户单元投入应用。读者可以参阅参考文献^[23，24]来获得更多的细节。

有些论文强调，为了利用内聚区单元得到更有意义的结果，应该通过有限元离散化来精确刻画裂纹扩展过程区的尺寸^[4，25]。在参考文献^[25]中，作者主张在过程区域中采用10个单元。但是在处理界面的脆断行为时，比如在典型的半导体应用中，需要在2D和3D应用中建立网格，这就严重限制了内聚区单元方法的应用。另外，界面的脆性和脱层的局域性可能会联合导致一些极限点（比如软化失稳或回折失稳）。但是，Van Hal等人^[24]证明，当使用传统的弧长控制方法，比如圆柱方法^[26]，小局部区域（比如说界面）将不可避免地产生极限点；而应用局部弧长控制方法，则能有效而精确地跳过这些极限点^[24]。

本研究对集成电路的后端结构建立了一个二维模型，该模型利用内聚力单元（并采用合适的界面韧度值）描述了后端结构内所有的界面，如图4.5a所示。图4.5b所示为力与位移的关系曲线，该曲线说明了集成电路的后端结构存在严重的回折失稳现象。而图4.6所示为一些典型的变形阶段（1，2，3）。

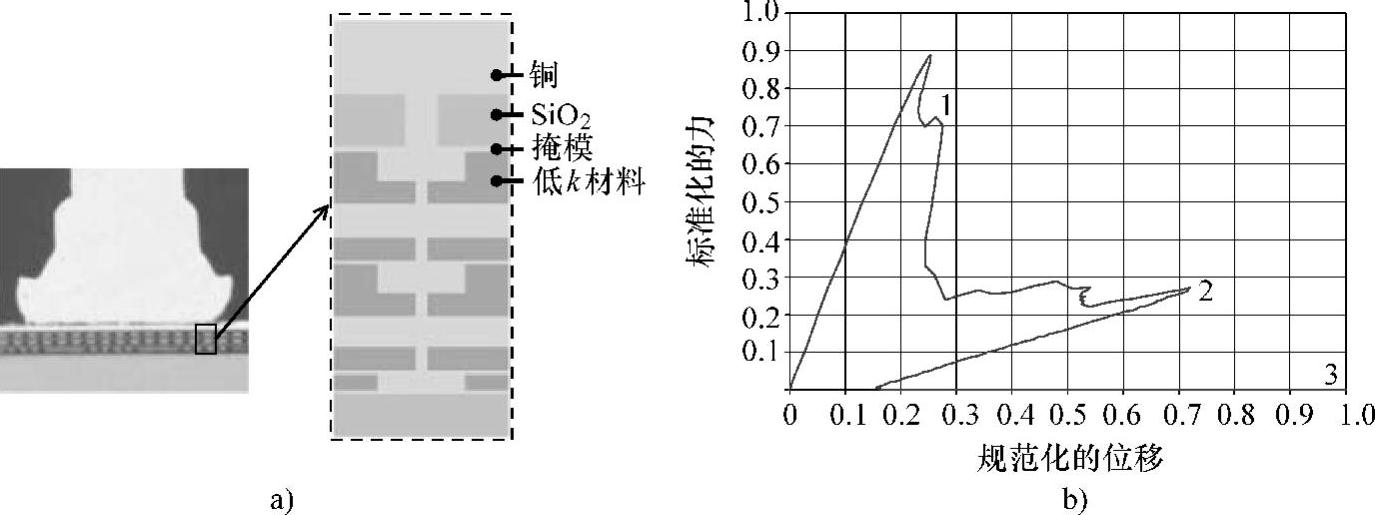
图4.5 二维IC后端模型，包括粘着区域

a）后端结构的横截面和相应的模型（放大图） b）力和位移的关系曲线，可以看到好几个极限点

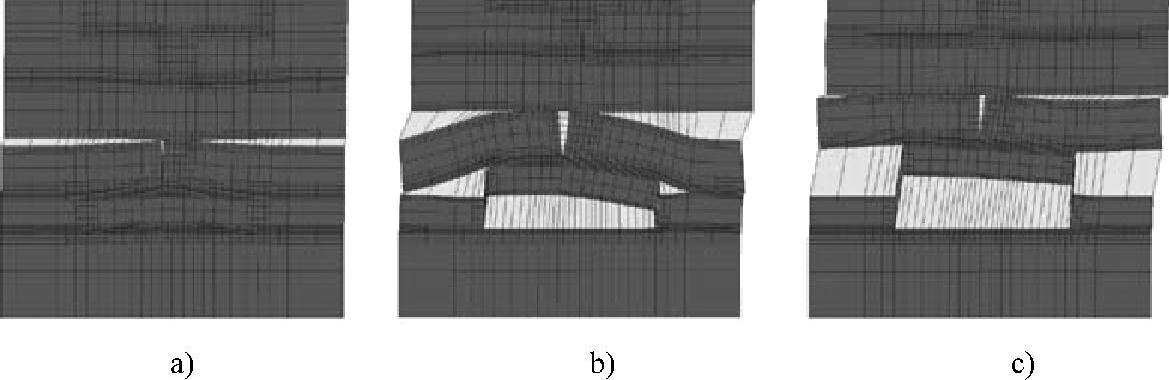
图4.6 后端结构脱层过程各阶段后端模型的局部区域放大图

a）对应图4.5b所示曲线的极点1 b）对应图4.5b所示曲线的极点2 c）对应图4.5b所示曲线的极点3

局部弧长控制方法应用前景广阔，因此研究人员正在把这种方法扩展到三维领域，以便能用该方法来研究实际的几何构型。