界面断裂力学优化探究

对于已给定几何形状和位置的、已经存在（或者假设存在的）的裂纹，断裂力学理论提供了一种方法来判断样品中的该裂纹是否已达到临界状态。为此，能量释放速率（Energy Release Rate，ERR），也称作裂纹驱动力，如在Griffith能量平衡式中所示，可以下式计算^[5]：

式中，W为外部功；U为弹性势能；Γ为裂纹生长需要的能量；a为裂纹长度。将式（4.1）左边除以样品厚度B，就得到了能量释放速率G（单位为J/m²）。而式（4.1）右边同样除以厚度B就能得到裂纹阻力的大小。裂纹生长的判断标准是G≥G_c，G_c是裂纹尖端的断裂韧度（单数）应力场。在界面断裂力学中，处理分层问题时，参数K是一个复杂变量，有K＝K₁+iK₂^[6]。由此得到的裂纹尖端应力为^[7]

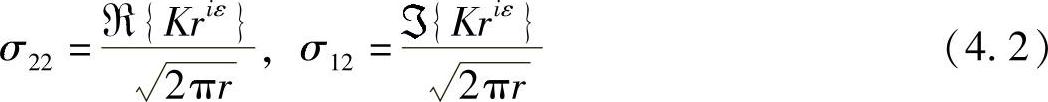
式中，σ₂₂为正应力；σ₁₂为剪切应力；r为裂纹尖端的距离；ε为双材料常数，其定义如下：

式中，β是第二Dundur参数。ERR是由下式的应力强度因子决定的：

式中，。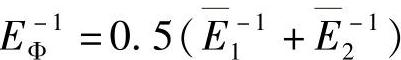

实验已证明，界面韧性是裂纹尖端处加载方向的函数G_c（ψ）。该函数的自变量是模式角ψ^[7，8]，模式角ψ定义为剪切力与法向拉力的比值，在裂纹尖端前参考距离为ℓ穿过界面进行传递，有(www.xing528.com)

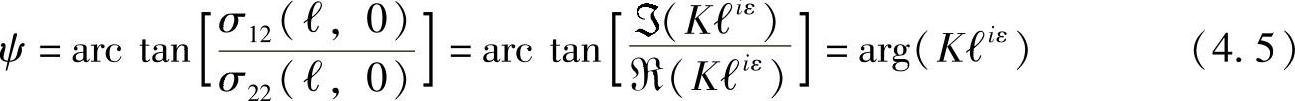
显然，在计算界面处的模式角时，需要选定参考长度值，因此在说明界面韧度值时，总是需要给定模式角。但是，由式（4.5）可得ψ₂＝ψ₁+εln（ℓ₂/ℓ₁），其中ψ_i与ℓ_i相对应，因此不同模式角对应的韧度值可以相互转化。

对线弹性材料进行有限元分析时，其ERR可通过所谓的J积分^[5]进行求解。为了计算J积分的精确值，就需要确定由表达式r^λ所表示的奇点的值，其中λ是奇点的次数。对于均质材料，λ＝0.5。Barsoum^[9]已经证明采用所谓的“四分之一点单元”能准确地表示奇点。但是，Abdel-Wahab和De Roeck^[10]也指出，除非有限元分析的网格非常细密，否则这个单元只能求解λ＝0.5时的奇点值。He等人^[11]也证明了这一点，他们认为采用有线元研究界面裂纹时，只有在网格非常细密的情况下，奇点的值才会收敛。

另外，也可采用其他方法来计算G，比如虚拟裂纹扩展方法^[12]和虚拟裂纹闭合方法^[13，14]。为了计算应力强度因子以便确定相应的模式角，人们已发展了几种计算方法，如Shih和Asaro^[15]提出的相互作用积分方法，以及采用裂纹尖端开放位移的裂纹表面位移方法^[16]。由于篇幅所限，本章不讨论这些方法。

因为界面韧性函数G（ψ）是有限元模型的输入量，故应对其测量。在标准的测试中，比如双悬臂梁（Double Cantilever Beam，DCB）、三点弯曲（Three-Point Bending，TPB）、四点弯曲（Four-Point Bending，FPB）测试中，模态混合度可通过改变样品的维数来改变。很显然，不同模式角需要不同的样品。为了使用单一样品刻画全部模态混合度内的界面，Thijsse等人^[8]提出了一种混合模式的弯曲装置。因为典型半导体器件的尺寸非常小，故人们对Reeder和Crews^[17]提出的装置进行了修改，以将其用于精确测量微小载荷。修改后的装置如图4.3所示。

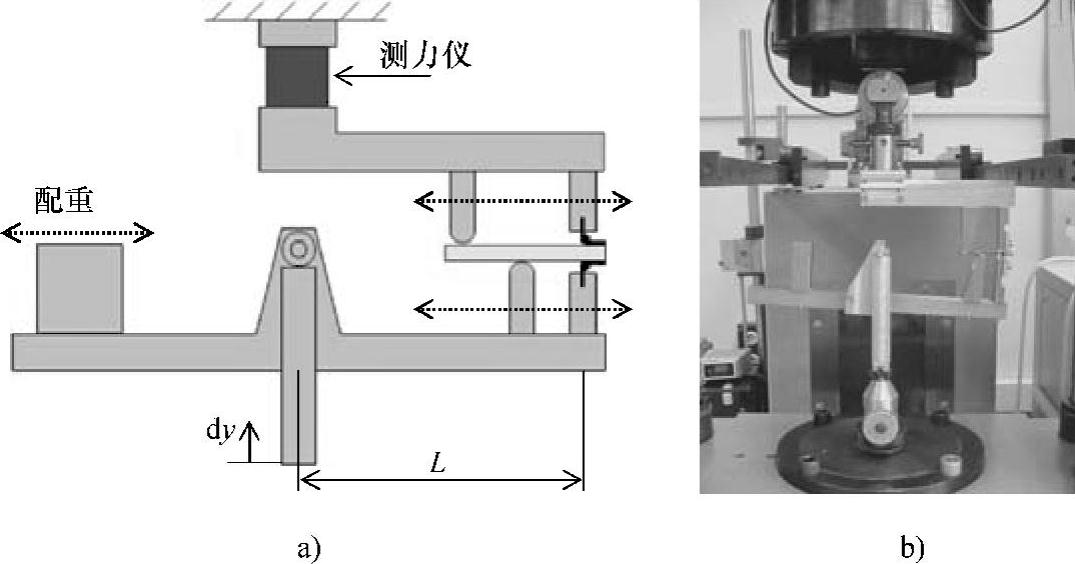
图4.3 混合模式的弯曲实验装置

a）装置示意图 b）实际装置图

改变施加在横梁L的力的位置能控制其模态混合度，因而进一步求解界面韧性函数G（ψ）。读者可从参考文献[8]获取更多信息。最近，Xiao等人^[18]提出了一种改进型混合模式弯曲装置。