锡焊膏印制工艺的CFD预测及混合分析方法探讨

模板印制工艺用于在PCB衬底的精确位置上沉积焊锡膏，以便为布置和焊接电子元器件做好准备。该工艺采用刮刀将焊锡膏涂抹到带有特殊开口形状的模具的表面。由于刮刀的作用，焊锡膏内会产生高压，这迫使焊锡膏填满模具的开口。

焊锡膏成分总体上会表现出非牛顿流变特性，如剪切变稀行为，即粘度随着剪切速率的增大而减小。这一行为使得焊锡膏，在因刮刀的移动导致剪切速率很高时，能以低粘度流入模具的开口中。当模具移开后，其粘度又因无剪切而增大，该现象可以帮助焊锡膏保持在适当的位置。

计算流体力学可以预测焊锡膏流过模具表面的运动过程。例如，可采用经典Navier-Stokes方程来模拟带有纳米颗粒的、以体积特性为特征的焊锡膏的涂抹运动过程，该焊锡膏采用下式所示粘度模型^[29]：

式中，η为表观粘度；η₀和η_∞分别为剪切速率为零和无限大时的粘度；λ为应变速率；K和m为实验获得的常数。图2.7给出了印制工艺的原理和通过经典连续介质法对焊料流动进行相关CFD预测的结果。

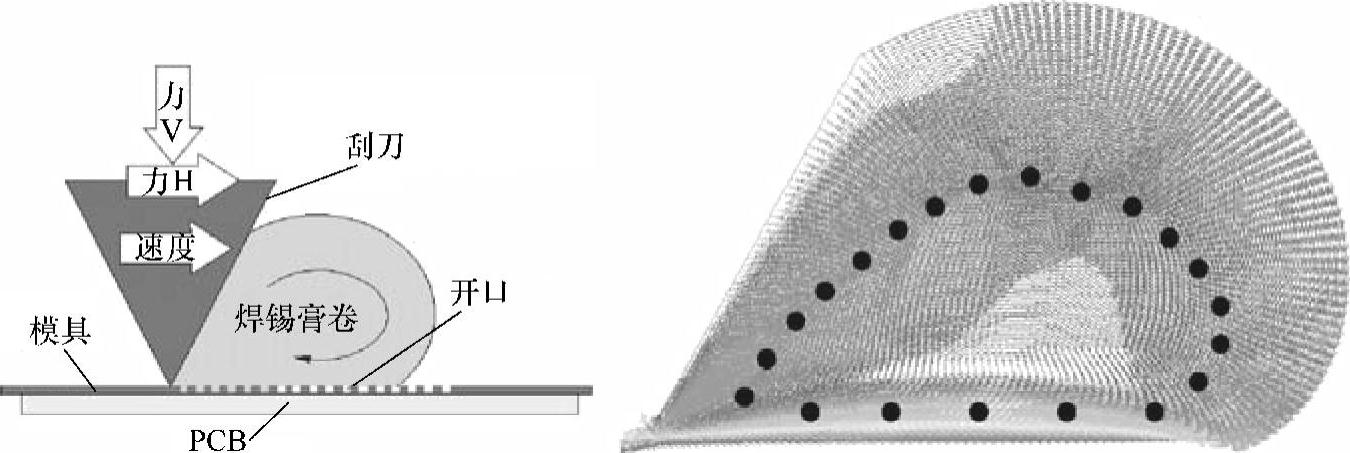
图2.7 模具印制中焊料流动的模拟预测

传统CFD模拟的基础是连续介质模拟法，并假设对象为均匀流体，且有可能无法获得单个焊料纳米颗粒输运的真实情况。要了解焊锡膏进入模板开口时的流动状况，就需要采用耦合了连续介质与离散颗粒的计算方法。(www.xing528.com)

Stokesian动力学方法^[30]和介观方法（如格子玻耳兹曼方法（Lattice Boltzmann Method，LBM）^[31]和耗散颗粒动力学（Dissipative Particle Dynamic，DPD）方法^[32]）均属于最引人注目的、基于离散颗粒的流体动力学计算技术。

Stokesian动力学方法只考虑固体颗粒之间的作用力，而不模拟悬浮液的具体流动情况。在该方法中，颗粒间相互作用力的基础是润滑理论。根据润滑理论，作用在一个颗粒的阻力取决于该颗粒与其相邻颗粒、固体壁面的相对位置和相对速度，以及该颗粒周围的悬浮液体的平均局部速度^[30]。该模拟方法缺少对悬浮液流动情况的详细模拟，且难以保证模拟过程遵循质量守恒定律，这些是其主要缺点。同时，与介观方法相比，Stokesian动力学方法对悬浮流动的模拟效果较差。

介观方法类似于分子动力学方法，但它采用一种假想颗粒代替了流体分子。这种假想颗粒比流体分子大得多，且足够代表真实的基本分子集团。因此，其需要的计算机内存要小些，碰撞时间也更接近宏观流动所需要的时间。通过设定假想颗粒的特性，可模拟宏观尺度下基本真实流体的流动过程。因为这些方法处于微观原子法与宏观连续介质法之间，所以它们被称为介观方法。耗散颗粒动力学（DPD）方法的根据是每个颗粒所受的吸引力和排斥力，这些力依赖于该颗粒相对于所有与之有关的颗粒的位置和速度。

研究人员尝试采用多尺度方法，即结合了纳米级动力学和连续介质宏观流动特性的混合模型，来更好地模拟锡焊膏印制工艺^[33]。图2.8左图所示为利用混合分析法对锡焊膏印制过程进行模拟的结果。其中，DPD模拟区的速度场通过填充的等高线图来表示，连续介质区和颗粒区在A-D窄带区重叠，如图2.8右图所示。A-D窄带区包含了已经定义的两个子区A-B和C-D，条状颗粒区域A-B与连续介质区的内边界相一致。相似地，条状连续介质区域C-D正好和颗粒模拟区域的外边界相符。该模拟测量并采用粗颗粒标示了条状颗粒区域A-B的质量和动量通量密度，并将测量结果强加在连续介质区的边界上。

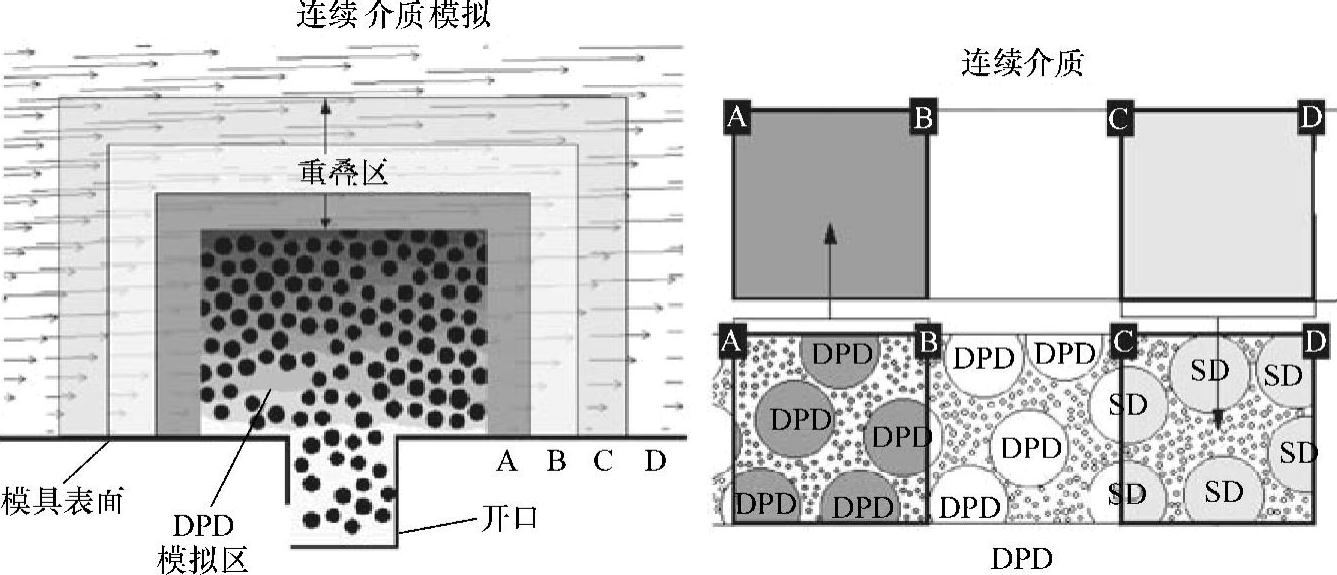
图2.8 采用DPD与连续介质方法的混合模型对流场进行二维模拟的结果