聚焦离子束工艺模拟优化方案

聚焦离子束（Focused Ion Beam，FIB）是微米或纳米尺度下在一个指定区域中去除将材料或是将材料沉积在其表面的一种铣削工艺。聚焦离子束的工作原理是采用高能镓离子Ga+（或其他离子）对目标表面进行撞击，使少量的材料以二次离子、自然原子和二次电子的形式溅射出去，从而实现在目标表面去除材料。

与其他传统方法相比，聚焦离子束工艺极大地降低了对受离子撞击表面的伤害。聚焦离子束工艺需控制的一个关键变量是深度变化值。该变量的正确控制对保证恰当地制造出三维纳米装置、微缩物体、各种微系统的外壳和模具都至关重要。

目前，研究人员已经开发出了一个数学模型，该模型可用来预测刻蚀形状或是计算达到预定形状所需要的停顿时间^[14，15]。该模型假设在目标表面存在一个正方形的像素矩阵。然后溅射模型被分布到该像素矩阵的每一个元素上，并由此建立了一个将任意像素（i，j）上溅射停顿时间t_ij与溅射深度H_ij联系起来的线性方程组。如下给出了该模型的简单描述。

如果（x_i，y_j）表示像素（i，j）的中心，那么因去除该像素上的材料而产生的溅射深度可以表示为

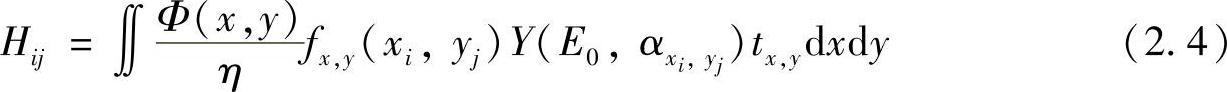
式中，H_ij为在点（x_i，y_j）处的溅射深度；Φ（x，y）为在点（x，y）处的离子通量（即每平方厘米上每秒通过的离子数目，单位是/（cm²·s））；η为目标材料的原子密度（每立方厘米的原子个数，单位是/cm³）；Y（E₀，α_xi，yj）为溅射产额（在点（x_i，y_j）处每个入射的离子所切除目标表面的原子数量）；t_x，y为点（x_i，y_j）处离子束的停留时间；f_x，y（x_i，y_j）为在两个维度上离子束的密度分布函数。

式（2.4）中的溅射产额是点（x_i，y_j）处离子束的入射角α_xi，yj、离子能E₀及离子源和目标材料的种类的函数。通常，溅射产额从垂直的离子束入射开始增加，在离子束入射角为60°～85°的范围达到最大值，随后由于临界入射下的强烈反射而迅速下降。下式是描述了溅射产额对入射角的依赖关系的经典经验公式，该公式由最初Yamamura^[16]提出，公式为

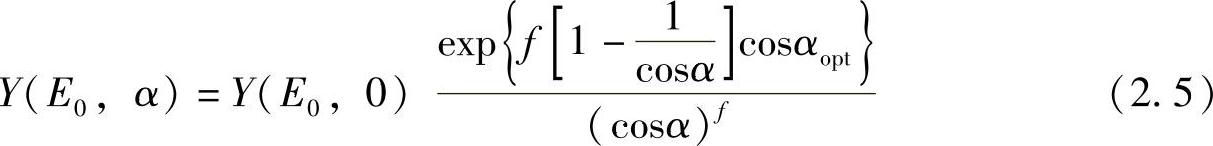
式中，Y（E₀，α）为以离子能E₀和名义入射角α入射时的溅射产额；f和α_opt用于拟合实验数据，且α_opt是获得最大溅射产额时的名义入射角。

式（2.4）的密度分布函数f_x，y（x_i，y_j）则体现了离子束的几何尺寸。即如果已经假定了二元高斯密度函数，那么

(www.xing528.com)

式中，r²＝（x_i-x）2+（y_j-y）²，用于定义聚焦在（x，y）上的离子束的径向坐标。

图2.3所示的聚焦离子束模拟示例采用了上述模型来预测离子的停顿时间和刻蚀形状。该示例采用上述模型计算出各个像素单元上的停顿时间，以便利用已给定参数的离子束溅射出一个含预定义的抛物线形状的腔体。该抛物线形状已预先定义，其最大深度为2μm。该示例分析假设离子束呈正态分布，其标准差σ＝0.075μm，Φ（x，y）＝1×10¹⁹个离子/（cm²·s），η＝5×10²²个原子/cm³，3μm×3μm的目标区域的像素网格是20×20。目标表面是硅材料，而溅射产额则是假定入射离子为20keV镓离子时利用式（2.5）计算得到的。

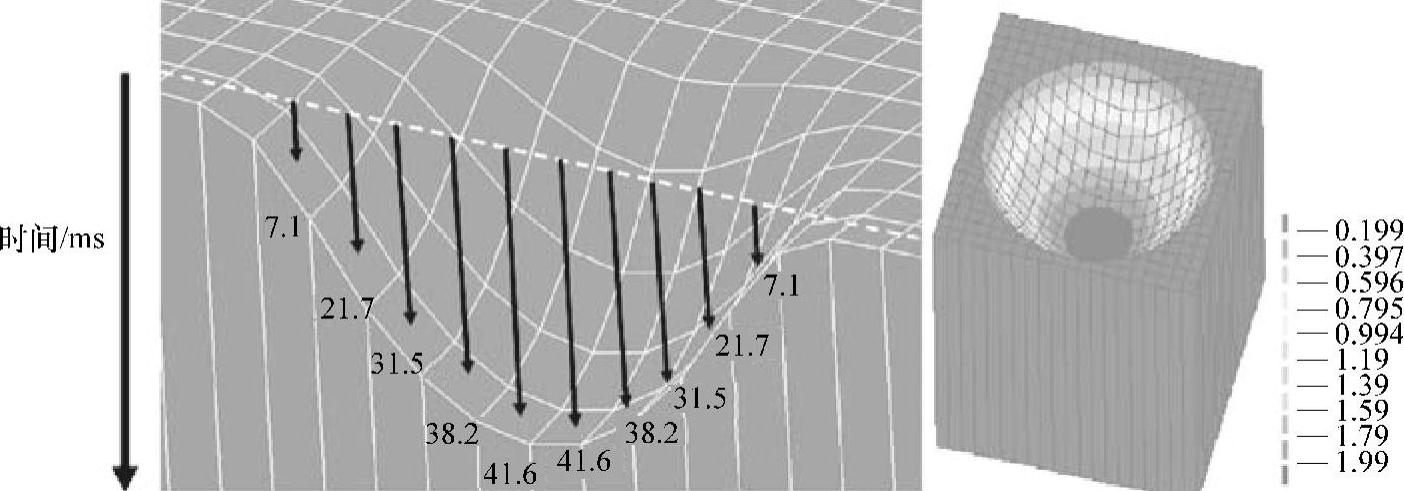
图2.3 对聚焦离子束研磨抛物线外形特征的建模

——材料横截面上各像素的研磨时间（左图）和等深线（单位为μm）

可通过考虑再沉积来改善上述的聚焦离子束溅射模型。式（2.7）给出的数学模型假设：从源像素单元（i，j）再次溅射到另一个目标像素单元（k，l）上的原子或离子的数量，取决于两个单元的相对位置与其各自的方向^[17]。材料的再沉积体积R_ij是溅射体积S_ij的函数，且可通过下式计算得到：

式中，β和γ分别是从源单元（i，j）的中心到目标单元（k，l）内任意可能位置所测得的最小和最大角度。并且，单元（k，l）上的再沉积体积是来自其他所有源单元（i，j）的再沉积量的总和。这个模型假设每个单元再沉积之后的总位移垂直于该单元的表面。

最近该领域的研究工作主要探讨如何模拟由离子束溅射过程造成的波痕层形成过程的非线性动力学特性^[18]。因为波纹层在各类纳米技术领域的应用潜力，模拟和理解波痕层的形成过程正日益受到人们的关注。