如何设计PID控制器的参数

PID 控制器三个环节中的三个参数， 即比例放大系数Kp、 积分系数Ki、 微分系数Kd 是设计PID 控制器的核心， 也是难点， 三个参数的选择决定了控制效果的优劣， 甚至决定了系统最终的稳定性。 下面介绍几种在工程中最常用的PID 控制参数设计方法。

1. 试凑法

试凑法是通过观察系统运行的状态来不断修改控制参数， 直到达到满意的运行状态的一种设计方法， 这种方法需要依靠设计人员丰富的设计经验来实行。 对于工程中很多复杂的不能够充分了解其模型的系统比较适合采取这种方法进行直接的控制。 在使用试凑法进行参数设计的过程中， 需要参考上述提到的性质： 增大比例放大系数可以加快响应， 但会引起更大的超调； 增大积分系数可以消除稳态误差， 但会降低稳定性； 增大微分系数可以增加稳定性并减少超调， 但会降低系统的抗干扰能力。

一般在试凑法中首先确定的是比例放大系数Kp： 在不考虑微分环节和积分环节的条件下， 可以由0 逐渐增大Kp 的值， 直到系统产生振荡； 反之减小Kp 的值， 直到系统振荡消失， 最终设置Kp 的值为当前值的60% ～70%。

接下来， 可以进行积分系数Ki 的设计： 首先设定一个较大的积分系数的值， 使之逐渐减小至系统振荡； 反之， 逐渐增大Ki 直到系统振荡消失， 最终取当前值的150% ～180%。

最终我们可以进行微分系数Kd 的设计， 设计过程与比例放大系数的设计过程类似， 最终可以取不振荡时值的30%。

在实际的工程应用中， 一般会使用PID 控制器三个环节中的两个， 其中比例放大环节是必要的， 可以选择积分环节组成PI 控制器， 或选择微分环节组成PD 控制器。 具体的设计方法需要根据工程实际和大量实践经验来确定。

2. 极点配置法

通过反馈控制可以改变闭环传递函数的全部或部分点的位置。 由于PID 控制中具有三个参数， 故只能改变固有传递函数为一阶或者二阶系统的全部极点来实现任意的极点配置。

首先， 我们讨论对于一阶系统， 应用极点配置法设计PID 控制参数的实现步骤。 对于一阶系统， 只需采用PI 或者PD 控制就可以实现任意的极点配置。

假设一阶系统的固有传递函数为

我们采用PI 控制， 取PI 控制的传递函数为

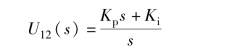
则反馈系统的闭环传递函数为

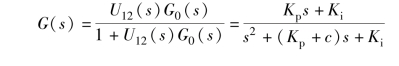
该闭环系统的特征多项式为

假设通过PI 或PD 控制后系统具有的期望阻尼比为ζ， 并且期望的无阻尼振荡频率为ωn， 则期望系统具有的特征多项式为

对比两个特征多项式， 最终可以得到所需的比例放大系数以及积分系数

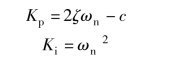
相对于一阶系统， 要实现二阶系统的任意极点配置， 就需要用到全部的PID 控制环节。假设二阶系统的固有传递函数为

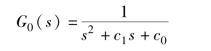
取PID 控制的传递函数为

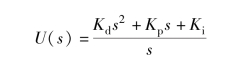
则系统的闭环传递函数为

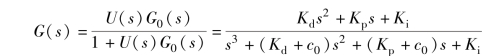
闭环系统的特征多项式为

假设期望系统具有的特征多项式为

对比两个多项式， 最终可以得到PID 控制器的设计参数为

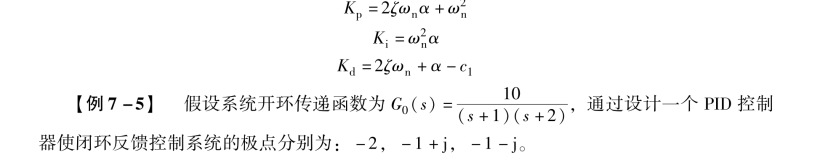
解： 设PID 控制器的开环传递函数为

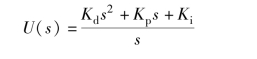
则反馈控制系统的闭环传递函数可以表示为(https://www.xing528.com)

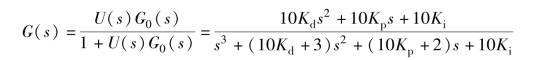
该反馈系统的特征多项式可以表示为

而配置几点之后， 期望系统的特征多项式为

使上述两个特征多项式相等， 即可获得设计所需的PID 控制参数

3. 根据频域特性要求设计PID 控制器

对于利用反馈控制的系统， 我们也可以根据对闭环系统频域特性的要求来设计PID 控制器。 假设， 要求加入PID 控制器后的闭环系统的截止频率为ωc， 相位裕度为γ。 设系统固有传递函数为G0（s）， PID 控制器的开环传递函数为U（s）， 则根据频域特性的定义可以得到

这样我们就可以得到PID 控制在期望截止频率的频域特性为

式中

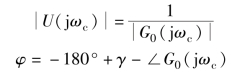
又因为PID 在截止频率处的频域特性可以推导为以下形式：

所以通过对比式（7.9） 和式（7.10） 可以最终得到设计所需的PID 控制参数

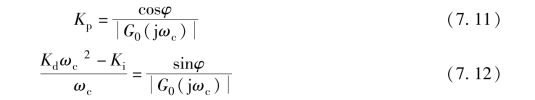
可以看出， 通过式（7.11） 可以唯一地得到比例放大系数Kp， 而积分系数Ki 和微分系数Kd 的设计则并不能由式（7.12） 唯一确定。 在很多设计实例中只用PI 控制或者PD 控制便可以比较方便地确定积分系数或者微分系数的具体取值。

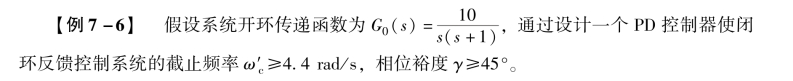
解： 在利用反馈控制以前， 可以计算得到该系统固有传递函数的截止频率ωc ＝3.1 rad／s，相位裕度γ ＝17.9°， 它们均不符合设计标准； 该系统固有开环传递函数的伯德图可由MATLAB 仿真得到， 如图7－28 所示。

假设， 我们将设计要求定为ω′c ＝4.4 rad／s， γ ＝45°； 又知该系统的固有开环传递函数的阻尼比ζ ＝0.158 1， 无阻尼振荡频率ωn ＝3.162 3 rad／s， 可以计算得到系统固有开环传递函数在设计要求的截止频率ω′c 处的频域特性为

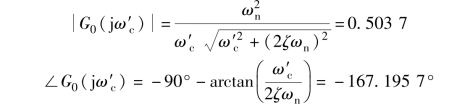
则可以计算得到PID 控制器的开环传递函数在设计要求的截止频率处的频域特性为

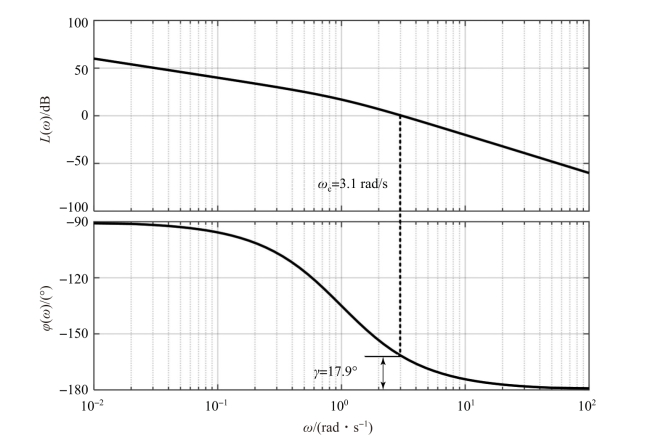
图7－28　系统固有开环传递函数的伯德图

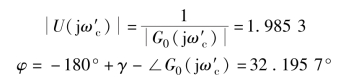
最后， 通过式（7.11） 以及式（7.12）， 可以计算得到设计所需的比例放大系数以及微分系数

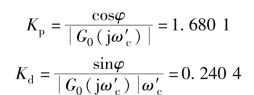
则PD 控制器的开环传递函数为

最终， 闭环反馈系统的开环传递函数为

通过MATLAB 仿真可以得到这个反馈控制系统的伯德图， 如图7－29 所示。

如图7－29 所示， 在加入我们设计计算的PD 控制器后， 闭环系统的频域特性得到了很大程度的改善， 其截止频率以及相位裕度都达到了理想的设计标准。 根据例7－6 所述， 我们可以通过系统的频域特性指标来便捷地设计PID 控制器， 从而达到理想的控制效果； 也可以从多种多样的PID 控制器设计方法中看出， PID 控制器的设计十分灵活便捷， 这使得PID控制器在实际工程中有着巨大的应用价值。

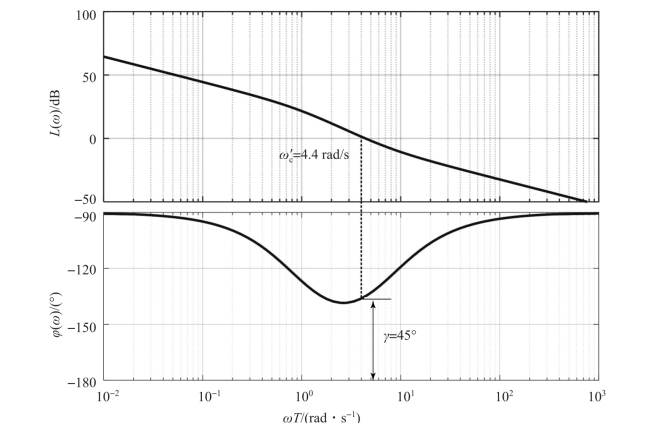
图7－29　PD 控制反馈系统的伯德图