探究PID控制系统的基本原理

PID 控制系统由PID 控制器、 执行机构以及被控对象组成。 PID 控制器主要包含了三个部分， 分 别 是 比 例 放 大 环 节 （Proportional）、 积 分 环 节 （Integral） 以 及 微 分 环 节（Derivative）。 PID 控制系统的基本原理如图7－19 所示。

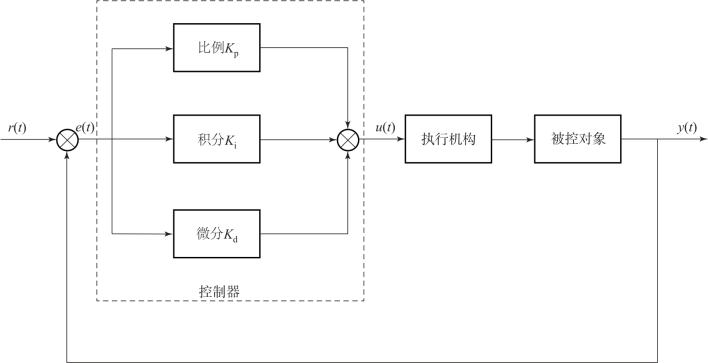
图7－19　PID 控制器的基本原理

将被控对象期望的状态作为输入， 将被控对象的真实状态作为输出， 将输出量反馈并与输入量做差就可以得到系统的状态偏差， 即

PID 控制器根据系统的状态偏差， 分别按照比例放大、 积分、 微分三个环节进行线性组合便构成控制指令u（t）， 执行机构按照控制指令来控制系统达到理想的状态。 PID 控制器的理想算法可以表示为

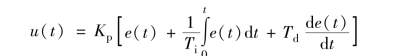
式中， Kp 为比例系数； Ti 为积分时间； Td 为微分时间。 由上式可以看出， 控制信号是由状态偏差e（t） 的比例放大、 对时间的积分量以及对时间的微分量构成的， 它充分利用了系统的偏差信息， 使得我们即使在不了解被控对象时， 也能通过偏差来实时地计算有效的PID 控制信号， 这也是PID 控制器得到广泛应用的原因之一。 我们可以将上式表达为更为直接的形式， 如

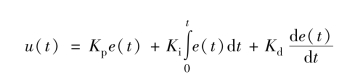
式中， Kp， Ki， Kd 分别代表了比例放大系数、 积分系数以及微分系数。 在工程应用中我们可以直接对这三个系数进行设计和快速的调节， 从而使得PID 控制器的使用十分方便快捷。将PID 控制写为传递函数的形式：

对比例放大环节、 积分环节和微分环节的选取将直接影响控制效果的优劣， 下面我们将逐一介绍这三个环节对于系统控制性能的影响。

1. 比例放大环节对系统控制性能的影响

引入比例放大环节可以及时地对系统产生的偏差做出修正。 当偏差产生时， 比例放大环节会立即对当时的偏差进行调节， 使系统快速向偏差减小的方向趋近。比例放大环节的算法可以表示为

传递函数可以表达为

2. 积分环节对系统控制性能的影响

引入积分环节是为了消除系统的稳态误差， 来保证系统对期望值实现没有误差的跟踪。积分环节取决于系统状态偏差对时间的积分， 这样即便系统存在很小的误差， 其对时间的积分也会不断增加， 随之积分环节的控制信号也会随时间增加， 从而驱动控制信号输出增大，使误差进一步减小， 直到消失。

积分环节利用并整合了偏差过去的信息， 其算法可以表示为

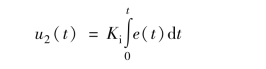
传递函数可以表示为

在实际工程应用中积分环节要配合比例放大环节共同使用， 并可以组成PI 控制器。 PI 控制器的传递函数为

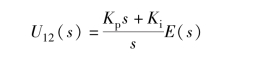
3. 微分环节对系统控制性能的影响

微分环节的作用主要是可以提高系统的响应速度和稳定性。 对系统的状态偏差进行微分可以预测偏差的变化趋势， 可以超前地对偏差进行控制， 在偏差还没有产生之时就抑制了偏差的产生与增加， 所以可以将其视作控制器对系统未来状态的作用。

微分环节的算法可以表示为

(https://www.xing528.com)

传递函数可以表示为

微分环节也要配合比例放大环节共同使用， 组成PD 控制器。 PD 控制器的传递函数为

解： 首先考察没有控制器时， 开环系统对输入信号的响应。 可搭建开环系统（图7－20）， 并给系统输入一个阶跃信号。 在MATLAB 软件中进行仿真， 开环系统在阶跃信号下的响应如图7－21 所示。

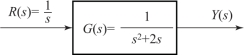
图7－20　例7－4 的开环系统结构图

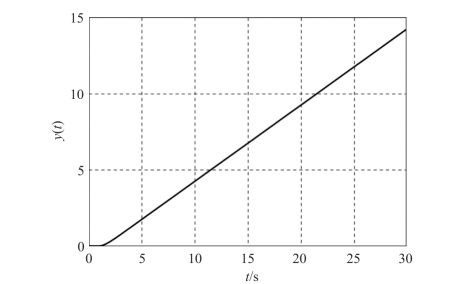
图7－21　开环系统在阶跃信号下的响应

根据图7－21 所示的仿真结果可知， 不加入控制器的开环系统是一个不稳定的系统， 随着时间的增加， 系统输出值逐渐发散。 为了能够使系统保持稳定， 我们加入比例放大环节（P 控制） 构成反馈控制系统。 加入P 控制后的闭环控制系统如图7－22 所示。 同样， 给系统输入阶跃响应， 并且将比例放大系数分别设置为： Kp ＝1， 5， 10， 在MATLAB 中进行仿真， 系统在阶跃信号下的响应如图7－23 所示。

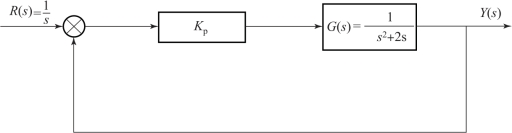
图7－22　加入P 控制后的闭环控制系统

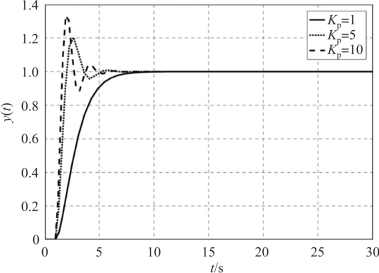
图7－23　P 反馈控制系统在阶跃信号下的响应

首先我们可以看出， 加入P 控制后， 系统的输出响应最终可以达到稳定。 但比例放大系数Kp 对系统稳定的过程有着很大的影响， 当Kp 增大时， PID 控制器的调节速度加快， 但同时系统的超调量也增加， 如果这个系数过大， 还可能导致整个系统发散。

接下来考察加入比例放大环节和积分环节（PI 控制） 后的反馈控制系统对阶跃信号输入的响应。 加入PI 控制后的闭环控制系统如图7－24 所示， 将比例放大系数设置为： Kp ＝1， 并分别设置积分系数为： Ki ＝0.1， 0.5， 1， 在MATLAB 中进行仿真， 系统在阶跃信号下的响应如图7－25 所示。

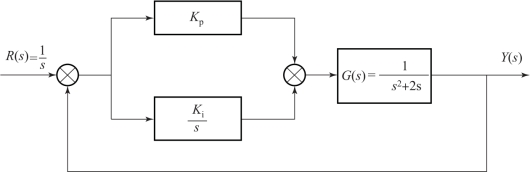
图7－24　加入PI 控制后的闭环控制系统

由图7－25 我们可以看出， 积分系数Ki 越大， 积分环节的作用也就会越显著。 积分环节的应用会使系统的稳定性下降， 同时动态过程变慢。

最后我们考察比例放大环节和微分环节（PD 控制） 对输入阶跃信号的闭环控制系统响应的影响。 加入PD 控制后的闭环控制系统如图7－26 所示； 同样， 将比例放大系数设置为： Kp ＝1， 并分别设置积分系数为： Kd ＝1， 5， 10， 在MATLAB 中进行仿真， 系统在阶跃信号下的响应如图7－27 所示。

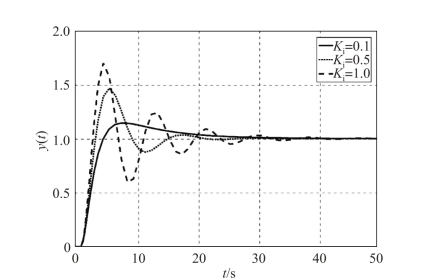
图7－25　PI 反馈控制系统在阶跃信号下的响应

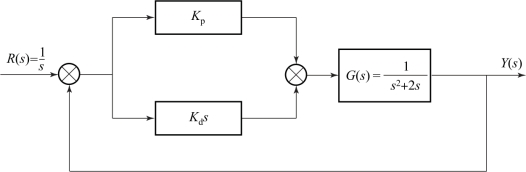
图7－26　加入PD 控制后的闭环控制系统

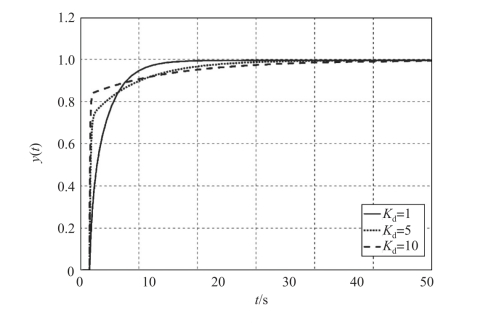
图7－27　PD 反馈控制系统在阶跃信号下的响应

由图7－27 我们可以看出， 微分环节的引入可以有效抑制系统的超调， 且微分系数Kd越大， 系统的响应越迅速， 但是收敛到稳定的时间越长。 选择合适的微分系数， 在微分环节的作用下系统的调节时间以及超调量都可以得到有效的减小。 但是， 微分环节的作用如果过大， 将减弱系统的抗干扰能力。

　从上面的仿真实例以及分析中我们可以看出， PID 控制器可以对系统进行有效的控制，在PID 控制器的作用下， 不稳定的系统可以达到期望的稳定位置并且动态过程也得到了很好的改善。 可见， 适当地设计PID 控制器参数对系统的控制有着决定性的影响。