串联滞后-超前校正方法优化

串联滞后－超前校正兼具二者的优点， 已校正系统响应速度快、 超调量小、 抑制高噪声的性能也不错。 若未校正系统不稳定， 而且对校正后的系统要求响应速度快、 稳态精度高、相位裕度大， 则采用串联滞后－超前校正最为合适。 串联滞后－超前校正装置通过利用超前部分增大系统的相位裕度， 利用滞后部分提高系统的稳态性能， 来实现良好的校正效果， 使系统满足性能指标的要求。

频域法设计串联滞后－超前校正的步骤归纳如下：

（1） 按照系统的稳态误差要求确定开环增益K。

（2） 按照开环增益K 绘制未校正系统的伯德图， 计算未校正系统的相位裕度和幅值裕度。

（3） 选择斜率从－20 dB／dec 变化为－40 dB／dec 的交接频率作为校正网络超前部分的交接频率。

（4） 选择系统截止频率和校正网络的α。

（5） 根据相位裕度， 预估校正网络滞后部分的交接频率。

（6） 校验已校正系统。

【例7－3】　系统的开环传递函数为

系统设计要求： 系统的速度误差常数Kv ＝10， 相位裕度γ≥45°。解： 首先求解系统的开环增益K。 由静态速度误差常数定义得

题设要求Kv ＝10， 则系统的开环增益K ＝40。

未校正系统的开环传递函数为

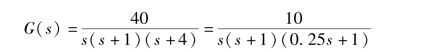
从而可得系统的闭环特征方程

(www.xing528.com)

应用MATLAB 绘制未校正系统的伯德图， 如图7－17 所示。 程序如下：

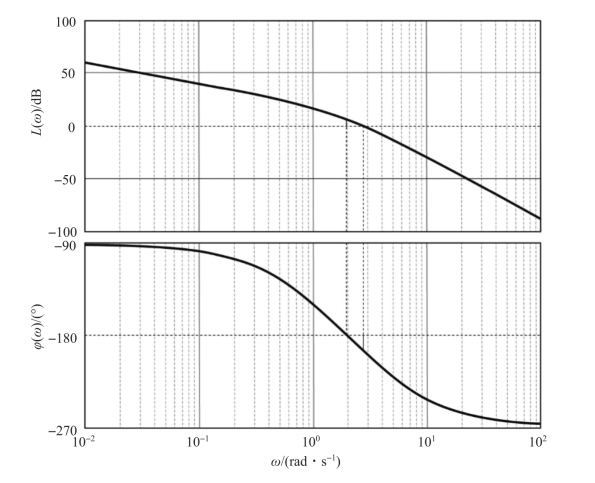
图7－17　未校正系统的伯德图

由图7－17 可知， 未校正系统的穿越频率ωx ＝2 rad／s， 对应的幅值裕度Kg ＝0.5 dB，截止频率ωc ＝2.779 7 rad／s， 对应的相位裕度γ ＝－15.011°。 由于幅值裕度大于零， 相位裕度小于零， 所以系统不稳定， 且闭环系统的带宽频率为3.897 1 rad／s。

由未校正系统的开环幅频特性曲线可知L′（ω′c） ＝L′（1.41） ＝14（rad／s）， 解得α≈7.08， 则滞后－超前校正网络的传递函数为

校正后系统的开环传递函数为

令s ＝jω， γ′＝45°， ω′c ＝1.41 rad／s， 解得Ta ＝22.4， 于是串联滞后－超前校正网络的传递函数为

应用MATLAB 绘制校正后系统的伯德图， 如图7－18 所示。 MATLAB 程序如下：

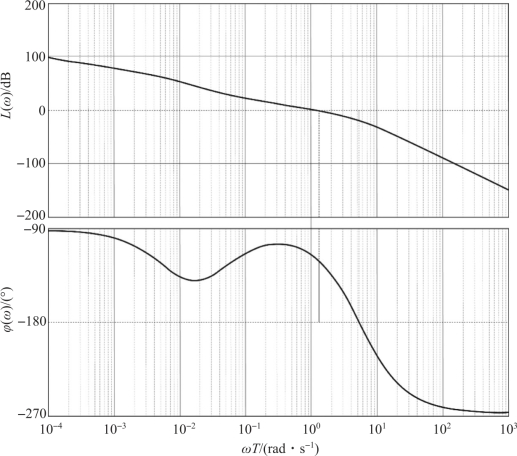
图7－18　校正后系统的伯德图

校正后系统穿越频率为5.282 4 rad／s， 相应的幅值裕度为7.728 4 dB， 截止频率为1.319 4 rad／s， 相应的相位裕度为59.527 9°， 满足性能指标要求。