串联滞后校正优化策略

利用滞后校正网络的高频幅值衰减特性， 使已校正系统在截止频率降低后获得足够的相位裕度是采用滞后校正网络进行串联校正的基本原理。 由此可知， 滞后校正网络的最大滞后角应尽量远离系统截止频率。 在对系统响应速度要求较低而对抑制噪声电平性能要求偏高时， 优先考虑采用串联滞后校正， 这种校正装置十分适合上述情况。 而且， 如果待校正系统已经具备了理想的动态性， 只是稳态性能未达到性能指标要求， 则也可以采用串联滞后校正装置来提高控制系统的稳态精度， 使各项指标满足设计要求， 并且保持系统的动态性能依然符合系统的要求。

利用频域分析法可以轻松地设计RC 滞后校正网络， 即只需要将校正网络的频率响应叠加到待校正系统的伯德图上， 就可以很方便地得到满足系统要求的频率响应。 在研究单位反馈最小相位系统时， 采用频域分析法设计串联无源滞后校正网络的步骤归纳如下。

（1） 按照系统的稳态误差要求确定开环增益K， 并画出未校正系统的伯德图。

（2） 计算未校正系统的相位裕度γ。

（3） 确定能够满足相位裕度设计要求的穿越频率， 且通常考虑滞后相位取5°。

（4） 配置滞后校正网络的零点。

（5） 根据穿越频率和未校正系统的对数幅频特性曲线确定期望的增益衰减。

（6） 由增益衰减－20lgα， 确定参数α。

（7） 计算滞后校正网络的极点频率， 完成无源滞后校正网络设计。

【例7－2】　未校正单位负反馈系统的开环传递函数为

系统的设计要求为： 系统的速度误差常数Kv ＝100。

解： 无源滞后校正网络可以通过改变系统的频率特性来获得满意的系统性能。 首先利用误差系数法确定系统的开环增益K， 计算如下：

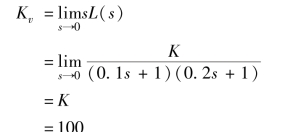
将K ＝100 代入传递函数有

然后， 求出待校正系统的相位裕度：

令φ（ω） ＝－180°， 确定相位裕度对应的相位截止频率ωc， 即

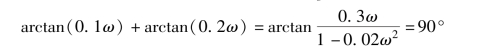
解得相位截止频率

则

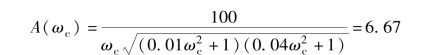
求解幅值裕度Kg， 得

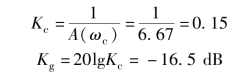
在增益穿越频率ω 处， 系统的开环频率特性的幅值是1， 即

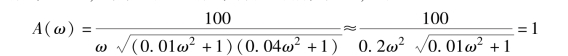
解得增益穿越频率ω≈16.7 rad／s， 则(www.xing528.com)

由φ（ω） 确定相位裕度γ， 得

绘制待校正系统的伯德图， 如图7－15 所示。 伯德图的MATLAB 程序如下：

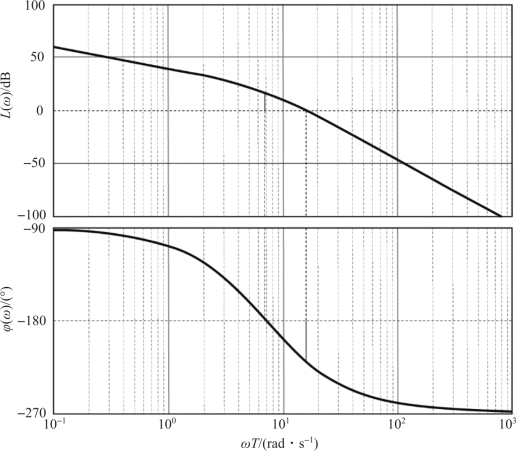
图7－15　未校正系统的伯德图

由图7－15 可知， 幅值裕度Kg ＝－16.5 dB， 相位裕度γ ＝－40.4°， 二者都小于零， 系统不稳定。 作－180° ＋γ ＝－13.8°直线， 与未校正系统的相频特性曲线交点的横坐标是ω′，计算解得ω′＝3.02 rad／s。 由于校正后系统截止频率较小， 可以取ε ＝10°， 则

所以， 作－128°直线， 与未校正系统相频特性曲线交点的横坐标为ω′c， 并计算解得

由

得参数α ＝0.026。

又由

解得T ＝94 s。 故， 确定滞后校正的传递函数为

校正后系统开环传递函数为

应用MATLAB 绘制校正后系统的伯德图， 如图7－16 所示。 对滞后校正网络进行验证，校正后系统的幅值裕度和相位裕度均大于零， 所以系统是稳定的， 满足性能指标的要求。 程序如下：

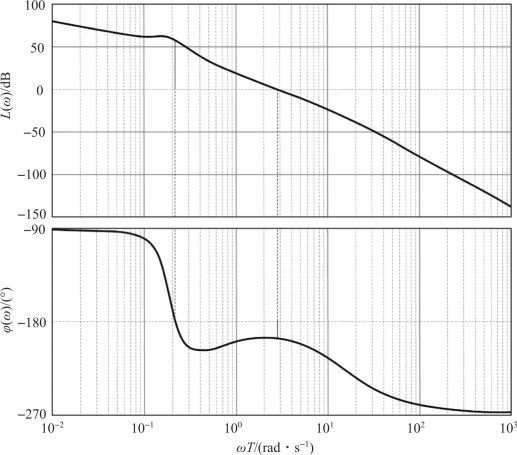
图7－16　校正后系统的伯德图

串联滞后校正和串联超前校正都能够实现反馈控制系统的校正设计， 它们的不同之处在于以下几个方面。

（1） 超前校正是运用超前装置的相位超前特性， 滞后校正是利用滞后装置的高频幅值衰减特性。

（2） 在控制系统设计中， 往往由于稳态增益的要求， 超前校正需要附加增益， 而滞后校正一般不需要。

（3） 超前校正的系统带宽往往大于滞后校正的系统带宽。