串联超前校正的应用和优化

利用超前校正网络的相位超前特性， 是串联超前校正的主要特点。 在进行超前校正网络设计之前， 应该首先根据对控制系统稳态误差的要求， 合理确定系统的开环增益， 之后即可绘制未校正开环系统的伯德图， 检验系统的截止频率和相位裕度是否满足要求。 若系统的相位裕度不够， 则可以把超前校正网络的伯德图在适当的位置和未校正系统的伯德图进行叠加， 从而将相位超前加到系统的相频特性曲线当中。

由超前校正网络的最大超前角表达式可知， 可以根据系统校正所需的最大超前角确定α的取值。 由于最大超前角出现在ωm 处， 为了充分利用超前校正网络的超前角， 需确保校正装置的频率ωm 恰好位于新的截止频率处， 此时可以根据在ωm 处超前校正网络的对数幅值10lgα 选择合适的频率ω′c， 且此处未校正系统的对数幅值为－10lgα， 此时即有ωm ＝ω′c， 根据这一条件即可进一步计算参数T。 无源超前校正网络的设计步骤归纳如下。

（1） 按系统的稳态误差要求确定开环增益K。

（2） 用开环增益K 计算未校正系统的相位裕度γ。

（3） 根据式（7.5） 计算系统的分度系数α。

（4） 计算10lgα， 确定未校正系统伯德图上幅值增益－10lgα （dB） 对应的频率ω′c， 即系统校正后的截止频率ω′c 和最大超前角频率ωm， 此时ωm ＝ω′c。

（6） 确定已校正系统的开环传递函数G（s）， 计算系统所需的最大超前角φm。

（7） 绘制校正后系统的伯德图， 验证已校正系统的相位裕度。

【例7－1】　单位反馈控制系统如图7－13 所示， 其开环传递函数为

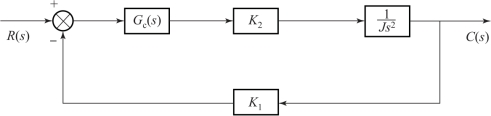
图7－13　单位反馈控制系统

解：

（2） 绘制K ＝10 的未校正系统的伯德图， 如图7－14 所示， 查出截止频率ω′c ＝3.084 2 rad／s、 相位裕度γ′＝17.964 2°和对数幅值L′（ω′c） ＝－8.129 1 dB。

（3） 由已知的开环截止频率ω′c≥4.4 rad／s， 试取ωm ＝5 rad／s， 且由

(www.xing528.com)

计算得α ＝6.5， 然后再由

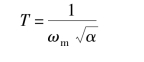
得T ＝0.078 4 s。

（4） 无源超前校正网络传递函数为

为满足开环频率特性函数的增益要求， 并使系统校正前后直流开环增益保持为10， 需要将增益放大6.5 倍。 所以， 已校正系统的开环传递函数为

在完成校正装置的设计后， 一般需要进行系统实际调校， 或者进行MATLAB 仿真来检查系统的时间响应特性。 此时， 为了保证仿真结果的精度， 需要将系统建模时忽略的部分尽可能地加入系统。 如果由于系统各种非线性因素的影响， 或者由系统噪声和负载效应等因素产生的干扰使已校正系统不能满足所有的性能指标要求， 则需要适当调整校正装置的形式或参数， 直到已校正系统满足全部性能指标为止。

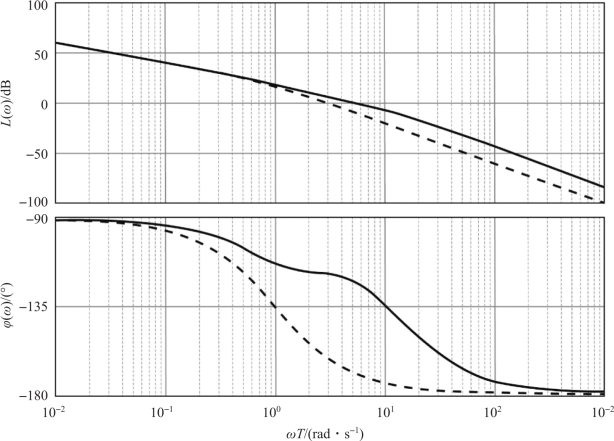
图7－14　校正前后系统的伯德图

应用MATLAB 绘制校正前后系统的伯德图程序如下：

应当指出， 在有些情况下采用串联超前校正是无效的， 它受以下两个因素的限制：

（1） 闭环带宽要求。 如果待校正系统不稳定， 为了得到规定的相位裕度， 则需要超前网络提供很大的相位超前量。 这会使分度系数α 的值必须选得很大， 继而造成已校正系统带宽过大， 使通过系统的高频噪声电平很高， 且很可能使系统失控。

（2） 在截止频率附近相位迅速减小的待校正系统， 一般不宜采用串联超前校正。 因为随着截止频率的增大， 待校正系统相位迅速减小， 使已校正系统的相位裕度改善不大， 很难得到足够的相位超前量。 在一般情况下， 这种相位迅速减小产生的原因是在待校正系统截止频率的附近有两个交接频率彼此靠近的惯性环节； 或有两个交接频率彼此相等的惯性环节；或有一个振荡环节。

在上述情况下， 系统可采用其他方法进行校正， 例如采用两级（或两级以上） 的串联超前网络（若选用无源校正网络， 中间需要串接隔离放大器） 进行串联超前校正， 或采用一个滞后校正网络进行串联滞后校正， 也可以采用测速反馈校正。