无源超前校正网络优化方案

如果一个校正网络的频率特性具有正的相位角， 则该校正网络称为超前校正网络。图7－5 所示为由电阻和电容构成的无源超前校正网络， 该网络的传递函数为

令

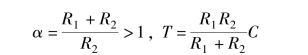
则式（7.1） 可改写为

图7－5　无源超前校正网络

由传递函数可知， 校正网络的设计问题可以转化为网络零点和极点的配置问题。 超前校正网络在s 平面上的零、 极点分布如图7－6 所示。 在图7－6 中， 可以通过改变α 和T 的值， 实现超前校正网络中的零、 极点在s 平面的负轴上任意移动。 由于α ＞1， 无源超前校正网络的负实极点总是位于负实零点的右侧， 且两点之间的距离由分度系数α 决定。 无源超前校正网络对应的幅频特性值和相频特性值可由下式计算：(www.xing528.com)

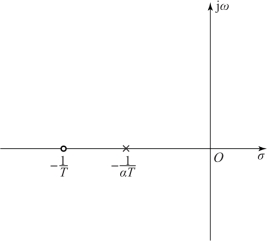
图7－6　无源超前校正网络的零、 极点分布

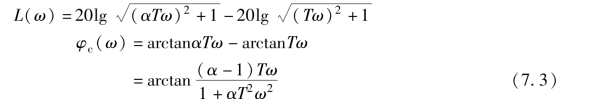
无源超前校正网络的伯德图如图7－7 所示。

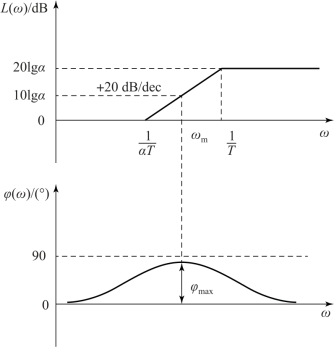
图7－7　无源超前校正网络的伯德图

式（7.4） 和式（7.5） 表明， 最大超前角φm 只和分度系数α 有关， α 越大， 超前作用越明显， 工程上实际选用α 的值一般不超过20。

上述分析表明， 超前校正网络具有高通滤波特性。 相对而言， 高频信号在通过超前校正环节时其幅值被放大及在高频段引入增益， 通常不利于系统的稳定。 然而， 超前校正网络在各频段都具有正的相位角， 这对控制系统的稳定性是有利的。 为了充分利用超前校正网络的校正功能， 同时避免其不利影响， 一般需要合理选择超前校正环节的参数（α 和T 的值），使其正的相位角在校正过程当中发挥主导作用。