开环不稳定系统与奈氏稳定性判定方法

【例6－8】　某系统的开环传递函数为

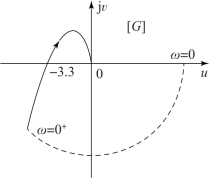
图6－38　例6－7 系统的开环幅相频率特性曲线

试利用奈奎斯特稳定性判据确定其稳定性。

解： 由于开环系统有一个极点在右半平面， 故P ＝1， 开环系统是不稳定的。 由传递函数可知， 该系统为非最小相位系统， 由一阶微分环节、 积分环节、 不稳定惯性环节组成。

讨论ω 由零变化到无穷大时各环节的幅角变化范围：

①一阶微分环节s ＋1： 0° ～90°。

由幅角的叠加原理可知， 开环系统ω 由零变化到无穷大时的幅角变化范围为－270° ～－90°。

系统开环频率特性为

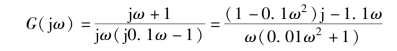
其幅频特性为

(www.xing528.com)

（2） 确定开环幅相频率特性曲线与实轴的交点。

令频率特性的虚部为零， 即

由于系统的幅角从－270°单调地增至－90°， 故幅相频率特性曲线在第三和第二象限内。利用MATLAB 程序绘制系统的开环幅相频率特性曲线的文本为：

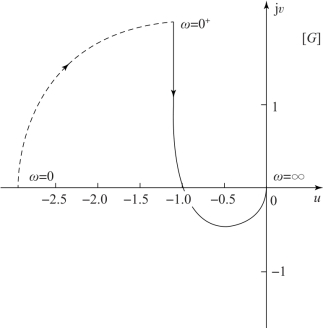
图6－39　开环不稳定系统的幅相频率特性曲线

从图6－39 中可以看出， 该系统的幅相频率特性曲线刚好穿过（－1， j0） 点， 由此认为其处于临界稳定状态。 分别令开环增益K ＝2， 0.5， 则该系统的幅相频率特性曲线如图6－40 所示。

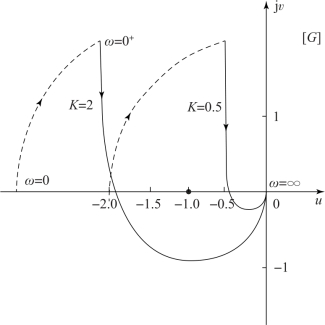
图6－40　K 值变化时的幅相频率特性曲线

从图中可以看出， 若增大开环增益K， 则幅相频率特性曲线与负实轴的交点为（－2，j0）， 开环系统幅相频率特性曲线先自下而上起于（－1， j0） 点以左的负实轴， 后又自上而下地穿过（－1， j0） 点以左的负实轴， 即得N ＝1／2， 则Z ＝P－2N ＝0， 闭环系统稳定。 同理， 若减小开环增益， 则N ＝－1／2， Z ＝P－2N ＝2， 说明闭环系统在右半平面有两个极点，系统不稳定。

上述结论可以用根轨迹法验证。 系统根轨迹如图6－41 所示。 从图中可以看出， K ＝1时， 系统处于临界稳定状态； 增大开环增益K， 系统稳定； K 减小， 则系统不稳定。

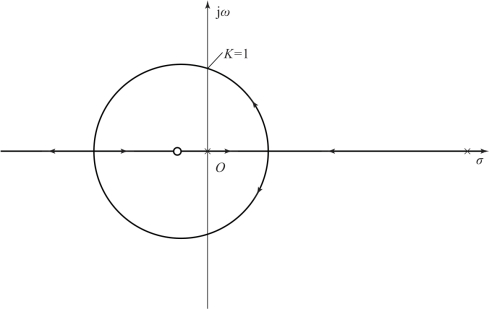
图6－41　系统根轨迹

对于本例中的开环不稳定系统， 右半平面极点的存在影响着包围的次数与不稳定闭环根的关系， 但是由于P ＝1， 因此奈奎斯特稳定性判据仍然适用。