幅角原理及其应用

已知系统的结构图如图6－32 所示。

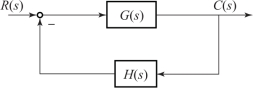
图6－32　系统结构图

设

则系统的闭环传递函数为

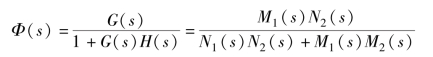
闭环特征多项式为

开环传递函数为

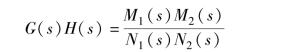
引入一个辅助函数F（s）， 令

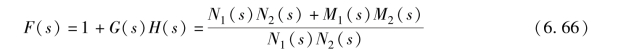
由式（6.66） 可知， F（s） 的分子是系统的闭环特征多项式D（s）， 分母则是系统的开环特征多项式。 在实际系统中， 开环传递函数分母的阶次n 必须大于或等于其分子的阶次m， 因而F（s） 可以写成如下形式：

式中， F（s） 的零点zi 为闭环传递函数Φ（s） 的极点， F（s） 的极点pj 为开环传递函数G（s）H（s） 的极点。 由式（6.67） 可知

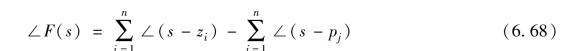(https://www.xing528.com)

由于s 是复数， 故F（s） 为复变函数， 它们分别可用复数平面上的矢量来表示， 所对应的复数平面分别称为s 平面和F 平面。 现研究s 在s 平面上沿一闭环曲线Γs 为路径取值时，F（s） 在F 平面上的变化情况。

当s 从s0 开始沿闭合路径Γs 顺时针移动一周时， 由式（6.68） 可得

假设F（s） 的零点和极点在复平面上的位置如图6－33 （a） 所示， 即闭环曲线Γs 内无零点和极点。 在这种情况下， 虽然F（s） 的幅角随s 的改变而改变， 但Δ∠F（s）总不会达到±2π。 这是因为当s 沿着Γs 旋转时， 构成∠F（s）的相角都在变化， 但由于没有零点和极点在闭环路径内， 它们的变化都没有超过±2π 就又回到了初值， 即

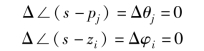
由式（6.69） 可知， Δ∠F（s） ＝0， 由此可知F（s） 在F 平面上的路径不会包围原点， 如图6－33 （b） 所示。

假设F（s） 的零点和极点在复平面上的位置如图6－33 （c） 所示， 即闭环曲线Γs 内有一个极点。 在这种情况下， 按照复变函数中矢量逆时针旋转时角度为正的规定， 若s0 沿闭合路径Γs 顺时针移动一周， 则有

当j≠3 时， 有

对于所有的i， 有

将以上结果代入式（6.69）， 即得Δ∠F（s） ＝2π， 即F（s） 在F 平面上会围绕坐标原点逆时针旋转一周， 如图6－33 （d） 所示。

同理， 假设F （s） 的零点和极点在复平面上的位置如图6－33 （e） 所示， 即闭环曲线Γs 内有一个零点。 在这种情况下， Δ∠F（s） ＝－2π， 即F（s） 在F 平面上会围绕坐标原点顺时针旋转一周， 如图6－33 （f） 所示。

一般情况下， 若Γs 内包含F（s） 的Z 个零点和P 个极点， 当s 沿Γs 顺时针取值时， 有

式（6.70） 表达的即为幅角原理的基本内容总结， 即一个复函数通过对闭合曲线进行映射得到的曲线会包围原点Z－P 次， 其中Z 和P 分别是函数在闭合曲线内的零点数和极点数。