二阶闭环系统频域指标与时域指标的关系探析

对于二阶系统， 其闭环传递函数为

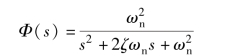
令s ＝jω， 得到闭环系统的频率特性为

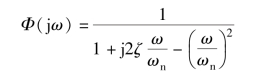
则系统的幅频特性为

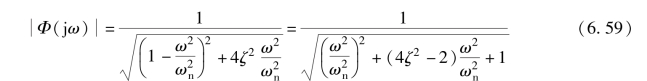
对于典型二阶系统， 谐振峰值Mr、 谐振频率ωr、 带宽频率ωb 与系统的阻尼比ζ、 无阻尼振荡频率ωn 有关。 下面对二阶闭环系统的频域指标与时域指标的关系进行讨论。

1. 谐振峰值与超调量的关系

达到谐振峰值时的频率即谐振频率， 为

由式（6.60） 可以看出， 谐振峰值Mr 与阻尼比ζ 有关。 系统的谐振峰值可以通过对系统进行频率响应实验得到， 然后由式（6.60） 就可以进一步估计出系统的阻尼比。

二阶系统的超调量为

由式（6.60） 和式（6.62） 可以看出， 谐振峰值Mr 以及超调量σP%都只与阻尼比有关，因此通过以阻尼比为参变量， 可以建立二者之间的关系。 以ζ 为参变量时， 超调量随谐振峰值的变化曲线如图6－30 所示。

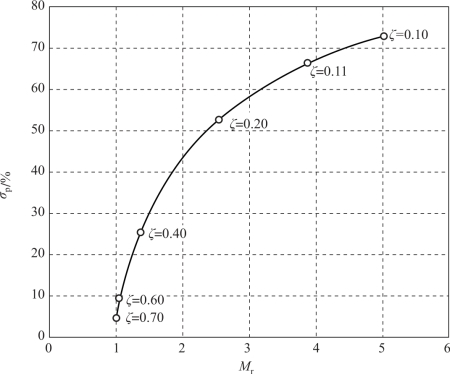
图6－30　超调量随谐振峰值的变化曲线(www.xing528.com)

超调量随谐振峰值的变化规律有明显的物理意义： 当闭环幅频特性有峰值时， 系统对信号有选择性， 它使信号频谱中在ω ＝ωr 附近的分量通过系统后显著增强。 因此， 当Mr 较大时， 系统的单位阶跃响应表现出接近ωr 的强烈振荡。

2. 带宽与上升时间的关系

求得带宽为

由式（6.63） 可知， 二阶系统的带宽与阻尼比ζ、 无阻尼振荡频率ωn 有关。

二阶系统的上升时间为

式中

若ωn 为常数， 以阻尼比ζ 为参变量， 则建立的带宽与上升时间的关系如图6－31 所示。

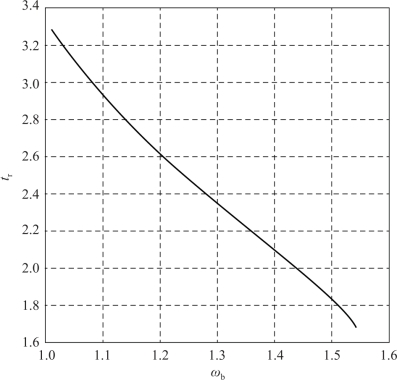
图6－31　带宽与上升时间的关系

从图中可以看出， 带宽越大， 上升时间就越小， 这说明系统的单位阶跃响应的速度和带宽成正比， 即带宽越大， 响应速度就越快。 对于任意阶次的控制系统， 这一关系仍然成立。

为了满足时域性能指标的要求， 通常对闭环频域指标提出如下要求：

（1） 谐振峰值相对较小。

（2） 系统的带宽相对较大， 从而使系统有较小的上升时间。