
若系统为最小相位系统, 且其频率特性的一般表达式为
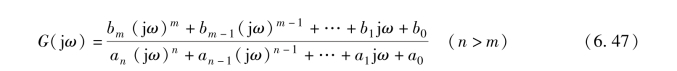
或写为各典型环节串联的形式
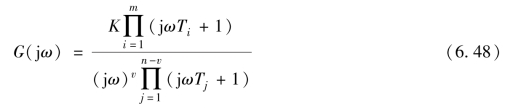
由式(6.48) 即可求得系统的幅频特性和相频特性, 其分别为
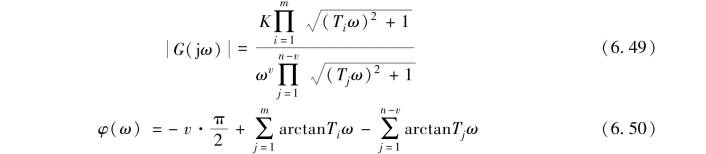
令式(6.50) 中ω =0 即可求得开环幅相频率特性曲线的起始角

由式(6.51) 和式(6.52) 可知, 对于式(6.48) 所示的系统, 开环幅相频率特性曲线的起始角仅与系统的型数即积分环节的个数v 有关; 终止角与开环传递函数分子和分母的阶数有关。 令式(6.49) 中ω→0 即可求得开环幅相频率特性曲线起点的幅值。 当系统为0 型系统, 即v =0 时, 幅相频率特性曲线起点的幅值为

2. 确定开环幅相频率特性曲线与实轴的交点
令开环系统频率特性的虚部等于0, 求取幅相频率特性曲线与实轴交点的频率ω1, 即
![]()
或令其相频特性为
![]()
求得与实轴交点的频率ω1 后, 将其带入频率特性的实部, 即可求得开环幅相频率特性曲线与实轴交点的横坐标为
![]()
3. 确定开环幅相频率特性曲线的象限和单调性
【例6-5】 设系统的开环传递函数为
![]()
试绘制系统开环幅相频率特性曲线。
解: 开环传递函数由两个惯性环节组成, 即
![]()
按如下步骤绘制系统的开环幅相频率特性曲线。(https://www.xing528.com)

(2) 确定开环幅相频率特性曲线与实轴的交点。
系统的开环频率特性为

由于惯性环节单调地由0°变化至-90°, 故该系统幅相频率特性曲线的变化范围为第三和第四象限, 系统的开环幅相频率特性曲线如图6-27 所示。
对于非最小相位系统, 需要根据开环系统中包含的各典型环节的特点, 分别计算它们的起始角和终止角, 然后利用式(6.14) 对各典型环节进行叠加, 最后确定开环系统幅相频率特性曲线的起点和终点。 确定系统与实轴的交点的步骤与最小相位系统相同。
【例6-6】 已知系统开环传递函数为
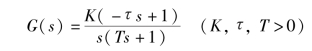
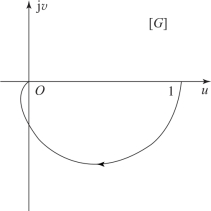
图6-27 例6-5 的开环幅相频率特性曲线
试绘制系统的开环幅相频率特性曲线。
解: 由传递函数可知, 该系统为非最小相位系统, 由比例环节、 非最小相位一阶微分环节、 积分环节、 惯性环节组成。
按如下步骤绘制系统的开环幅相频率特性曲线:

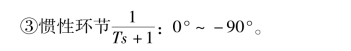
由相角的叠加原理可知, 开环系统ω 由零变化到无穷大时的相角变化范围为-90° ~-270°。
系统开环频率特性为
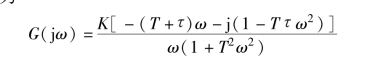
其幅频特性为
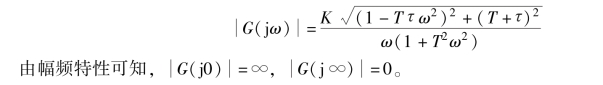
(2) 确定开环幅相频率特性曲线与实轴的交点。

令频率特性的虚部为零, 即由于系统的相角从-90°单调地减至-270°, 故幅相频率特性曲线在第三和第二象限内, 开环幅相频率特性曲线如图6-28 所示。
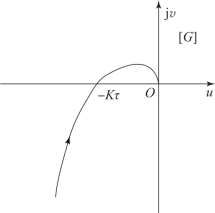
图6-28 例6-6 中系统的开环幅相频率特性曲线
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




