典型环节的幅相频率特性曲线解析

1. 比例环节G（jω） ＝K

比例环节的幅频特性和相频特性为

将频率特性用实部和虚部表示为

由式（6.31） 和式（6.32） 可知， 比例环节的频率特性与频率ω 无关， 它是复平面内的一个固定点。 其幅相频率特性曲线如图6－19 所示。积分环节的幅频特性和相频特性为

将其改写为实部和虚部的形式即为

当ω 从零变化至无穷大时， 由式（6.33） 可知， 幅频特性由无穷大变化至零， 相频特性与ω 无关， 始终为－90°； 由式（6.34） 可知， 其实部始终为零， 虚部从负无穷大变化至零。积分环节的幅相频率特性曲线如图6－20 所示。

图6－19　比例环节的幅相频率特性曲线

图6－20　积分环节的幅相频率特性曲线

3. 微分环节G（jω） ＝jω

幅频特性和相频特性为

将其改写为实部和虚部的形式即为

当ω 从零变化至无穷大时， 由式（6.35） 可知， 幅频特性由无穷大变化至零， 相频特性与ω 无关， 始终为90°；而由式（6.36） 可以看出， 其实部始终为零， 虚部由零变化至无穷大。 微分环节的幅相频率特性曲线如图6－21所示。

图6－21　微分环节的幅相频率特性曲线

用虚部除以实部， 进一步得

将式（6.38） 代入式（6.37）， 消去Tω 项， 即得

将式（6.39） 改写为如下形式：

由式（6.40） 可知， 惯性环节的幅相频率特性曲线是圆心为（1／2， j0）、 半径为1／2 的圆。惯性环节的幅相频率特性曲线如图6－22 所示。(www.xing528.com)

5. 一阶微分环节G（jω） ＝jTω ＋1

幅频特性和相频特性为

其实部和虚部分别为

由式（6.42） 可知， 当ω 从零变化至无穷大时， 其实部保持不变， 始终为1， 其虚部由零变化至无穷大。 一阶微分环节的幅相频率特性曲线如图6－23 所示。

图6－22　惯性环节的幅相频率特性曲线

图6－23　一阶微分环节的幅相频率特性曲线

幅频特性和相频特性为

图6－24　振荡环节的幅相频率特性曲线

幅频特性和相频特性为

将惯性环节的频率特性写成实部和虚部的形式即为

其实部和虚部分别为

将式（6.44） 变换后可得

延时环节的幅频特性和对数相频特性为

其幅相频率特性曲线是以原点为圆心、 以1 为半径的圆， 如图6－26 所示。

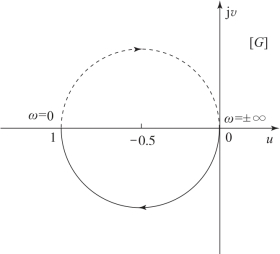
图6－25　不稳定惯性环节的幅相频率特性曲线

图6－26　延时环节的幅相频率特性曲线