典型环节的对数频率特性分析

1. 比例环节

比例环节的传递函数为

其频率特性为

其对数幅频特性和对数相频特性为

比例环节的伯德图如图6－6 所示。

图6－6　比例环节的伯德图

（a） 幅频特性曲线； （b） 相频特性曲线

2. 积分环节

积分环节的传递函数为

其频率特性为

其对数幅频特性和对数相频特性为

由于伯德图的横坐标按lgω 均匀分度， 因此可认为对数幅频特性的自变量为lgω， 从而可得对数幅频特性曲线的斜率

令L（ω） ＝0， 可得ω ＝1。 故积分环节的对数幅频特性曲线为一条直线， 其斜率是－20 dB／dec，与0 dB 线的交点为ω ＝1； 其对数相频特性恒为－90°。

积分环节的伯德图如图6－7 所示。

3. 微分环节

微分环节的传递函数为

其频率特性为

图6－7　积分环节的伯德图

（a） 幅频特性曲线； （b） 相频特性曲线

其对数幅频特性和对数相频特性为

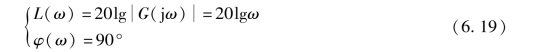
由式（6.19） 和式（6.18） 可以看出， 微分环节与积分环节的对数幅频特性和对数相频特性都只差一个负号， 因此他们的伯德图关于ω 轴对称。 微分环节对数幅频特性曲线的斜率为20 dB／dec， 与横轴的交点为ω ＝1； 对数相频特性恒为90°。

微分环节的伯德图如图6－8 所示。

图6－8　微分环节的伯德图

（a） 幅频特性曲线； （b） 相频特性曲线

4. 惯性环节

惯性环节的传递函数为

其频率特性为

其对数幅频特性和对数相频特性为

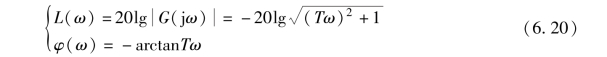
注意： 当Tω≤1， 即ω≤1／T 时， L（ω）≈0 dB， 它是一条斜率为0 的直线； 当ω≥1／T时， L（ω）≈－20lgTω ＝－20（lgT ＋lgω）， 它是一条斜率为－20 dB／dec 的直线。 这两条直线即为对数幅频特性渐近线， 由这两条直线构成的折线称为惯性环节的对数幅频特性渐近线，这两条直线的交点ω ＝1／T 称为交接频率。

惯性环节的伯德图如图6－9 所示。

图6－9　惯性环节的伯德图

（a） 幅频特性曲线及对数幅频特性渐近线； （b） 相频特性曲线

5. 一阶微分环节

一阶微分环节的传递函数为

其频率特性为

其对数幅频特性和对数相频特性为(www.xing528.com)

比较式（6.21） 和式（6.20） 可知， 一阶微分环节的对数频率特性是惯性环节对数频率特性的负值， 即一阶微分环节和惯性环节的对数幅频特性与对数相频特性分别关于ω 轴对称。

一阶微分环节的伯德图如图6－10 所示。

图6－10　一阶微分环节的伯德图

（a） 幅频特性曲线； （b） 相频特性曲线

6. 振荡环节

振荡环节的传递函数为

其频率特性为

其对数幅频特性和对数相频特性分别为

当ω／ωn≪1， 即ω≪ωn 时， 由0 ＜ζ ＜1 可得

这表明， 低频段的渐近线是一条零分贝的直线， 即与横轴重合。

当ω／ωn≫1， 即ω≫ωn 时， 可得

这表明， 高频段是一条斜率为－40 dB／dec， 且与横轴相交于ω ＝ωn 的直线。

上述两条直线即为振荡环节的对数幅频特性渐近线， 这两条直线相交于ω ＝ωn， 此频率称为振荡环节的交接频率。

在上述近似过程中， 忽略了阻尼比ζ 的影响。 但是精确的伯德图随阻尼比ζ 的变化而变化， 精确的曲线可以根据式（6.22） 绘制。 二阶振荡环节在阻尼比不同时的伯德图如图6－11所示。

图6－11　二阶振荡环节在阻尼比不同时的伯德图

（a） 幅频特性曲线及对数幅频特性渐近线； （b） 相频特性曲线

从图中可以看出， 对数幅频特性渐近线与精确的对数幅频特性曲线的形状大致相同， 但在交接频率ωn 附近产生误差， 且阻尼比的不同会影响对数幅频特性渐进线与准确的对数幅频特性曲线之间的误差。

定义对数幅频特性与渐近特性之间的误差为

根据式（6.24） 绘制不同阻尼比对应的误差曲线， 如图6－12 所示。

图6－12　对数幅频特性误差曲线

7. 不稳定惯性环节

不稳定惯性环节的传递函数为

其频率特性为

其对数幅频特性和对数相频特性为

不稳定惯性环节的伯德图如图6－13 所示。 由图可知， 不稳定惯性环节的对数幅频特性曲线与惯性环节的对数幅频特性曲线一致。

8. 延时环节

图6－13　不稳定惯性环节的伯德图

（a） 幅频特性曲线； （b） 相频特性曲线

对式（6.27） 两端进行拉普拉斯反变换， 并令初始条件为零， 可得延时环节的传递函数为

其频率特性为

其对数幅频特性和对数相频特性为

延时环节的伯德图如图6－14 所示。 由图可知， 延时环节的对数幅频特性是与横轴重合的直线， 对数相频特性随ω 的增加而增加。

图6－14　延时环节的伯德图

（a） 幅频特性曲线； （b） 相频特性曲线