频率特性基本概念解析

设线性定常系统传递函数如下：

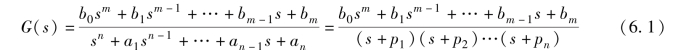
式中，－p1，－p2， … ，－pn 为传递函数G （s） 的n 个互异极点， 它们可能是实数或共轭复数。

对于传递函数为G（s） 的系统， 设输入信号r（t） ＝Asinωt， 则该输入信号的拉普拉斯变换为

由传递函数即可求得系统的输出信号

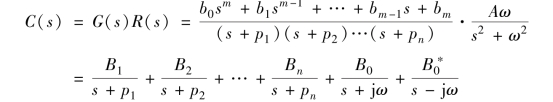
对式（6.2） 进行拉普拉斯反变换， 得到系统的时域响应n

频率特性与传递函数、 微分方程一样， 也是一种表示系统特性的数学模型。 三者之间的关系如图6－1 所示， 图中的p ＝d／dt 为微分算子。

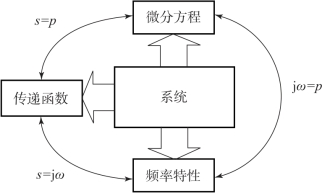
图6－1　频率特性、 传递函数、 微分方程之间的关系

【例6－1】　对于一阶惯性环节， 其传递函数为

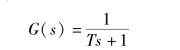(www.xing528.com)

取T ＝1， 输入信号为r（t） ＝sin2t， 试求该系统输出响应曲线、 稳态输出响应曲线。

解： 首先求出输入信号的拉普拉斯变换

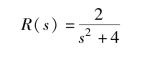
则输出信号可表示为

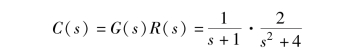
对上式进行拉普拉斯反变换， 即可求得输出信号的时域响应

除了利用拉普拉斯变换和拉普拉斯反变换外， 也可以直接利用传递函数求得系统的稳态输出。 令s ＝jω， 则可得系统的频率特性

由幅频特性的定义可求得系统的幅频特性为

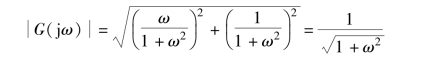
相频特性为

式（6.9） 和式（6.10） 表明， 用两种方法求得的系统稳态输出相同。 该系统输出响应曲线、 稳态输出响应曲线与输入曲线的对比如图6－2 所示。

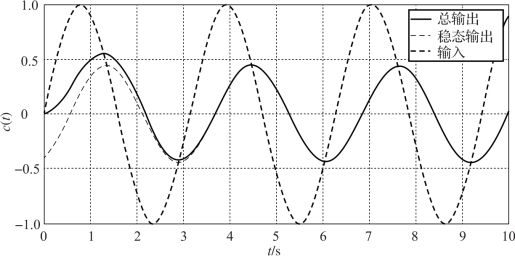
图6－2　输出响应曲线、 稳态输出响应曲线与输入曲线的对比