控制系统设计实例：超前校正网络与闭环系统稳态误差解决方案

【例5－13】　为了对自动焊接头进行精确定位， 需要设计具有良好性能的控制系统。自动焊接头的位置控制系统的结构图如图5－27 所示。 图中， 放大器增益K1 和测速反馈系数K2 待定。 试利用根轨迹法选择参数K1 和K2， 使系统满足如下性能指标：

（1） 在斜坡输入作用下， 系统的稳态误差不大于输入信号幅值的35%。

（2） 主导极点的阻尼比满足ζ≥0.707。

（3） 调节时间（Δ ＝2%）≤3 s。

图5－27　自动焊接头位置控制系统的结构图

解： 由图5－27 可知， 系统的开环传递函数为

闭环传递函数为

闭环传递函数特征多项式的三个系数均大于零， 系统是恒稳的。 速度误差系数为

为达到性能指标（1）， 应满足

显然， 为提高闭环系统的稳态性能， 应选取较大的K1 和较小的K2。

性能指标（2） 要求闭环系统的特征根落在左半复平面的45°线之下， 而性能指标（3）可转化为对主导极点实部大小σ 的要求， 即

这要求σ≥1.47。 为满足性能指标要求， 应当使闭环系统的主导极点落在图5－28 所示的阴影区域中。

图5－28　闭环极点的可行区域

令α ＝K1， β ＝K1K2， 则可将闭环系统的特征方程整理为

首先考虑参数α ＝K1 的选择。 令β ＝0， 则α 变化时的根轨迹方程为

绘制出的相应根轨迹， 如图5－29 （a） 所示。 初步选定α ＝K1 ＝20， 在图中标注出相应的极点。

再来考虑β 的取值。 在闭环系统特征方程式（5.78） 中代入α ＝20， 则β 变化时的根轨迹方程为

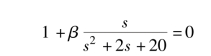
绘制出相应的根轨迹， 如图5－29 （b） 。 当β ＝4.33， 即K2 ＝0.22 时， 即可得到满足阻尼比要求的闭环极点s1，2 ＝－3.16 ±j3.16。

图5－29　例5－13 的根轨迹

至此， 已经确定参数K1 ＝20， K2 ＝0.22。 闭环系统稳态误差与输入的斜坡信号幅值之比满足

调节时间满足

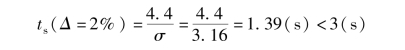
因此， 参数K1 和K2 的设计值能够使系统满足全部指标要求。 作出的系统的单位阶跃响应曲线以及单位斜坡响应曲线， 如图5－30 所示。

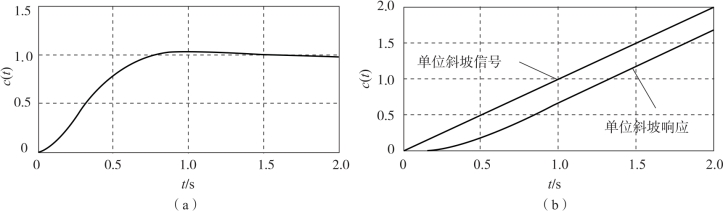
图5－30　例5－13 中控制系统的单位阶跃响应曲线和单位斜坡响应曲线

下面给出例5－13 的MATLAB 程序：

【例5－14】　某控制系统结构图如5－31 所示， 且有

式中， K 为可变参数。

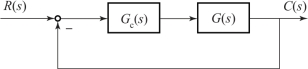
图5－31　例5－14 的控制系统结构图

（1） 假定Gc（s） ＝1， 绘制出K 由零变化至正无穷时的根轨迹。

（2） 出于对系统稳态性能的要求， 选定K ＝5。 确定此时闭环系统的极点及阻尼比、 无阻尼振荡频率。

（3） 仍然选定K ＝5。 为提高系统的动态性能， 请根据以下性能指标设计Gc（s）。(www.xing528.com)

①闭环主导极点具有阻尼比ζ ＝0.5 以及无阻尼振荡频率ωn ＝3rad／s。

②不可使系统的稳态性能降低， 应保证速度误差系数Kv 不小于5。

解：

（1） 此时的根轨迹方程为

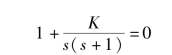
根据上式， 画出K 由零变化至正无穷时的根轨迹， 如图5－32 所示。

（2） 闭环系统的特征方程为

图5－32　例5－14 原系统的根轨迹

（3） 性能指标给定了对阻尼比和无阻尼振荡频率的要求， 主导极点可由下式得到

从中解得s1，2 ＝－1.50 ±j2.60。

由图5－32 可知， 若Gc（s） 为比例控制器， 则仅调整开环增益是无法满足设计要求的，故需要引入校正网络。 分析性能指标要求， Gc（s） 的设计是为了提高系统的动态性能， 对于稳态性能只需保持原来的水平即可。 根据5.3 节中对附加开环零、 极点作用的分析， 本题需要选择超前校正网络来改变根轨迹的走向， 使其经过满足要求的闭环主导极点。 下面对超前校正网络的具体参数进行设计。

设计超前校正网络参数的一般流程： 首先计算出从原系统开环零、 极点到理想的闭环极点的向量辐角， 然后计算超前校正网络所需提供的辐角φ， 从而使辐角条件在理想闭环极点处成立。 如果角度φ 过大以至于单个超前校正网络无法提供， 那么将需要设计两个或两个以上的超前校正网络。

假定超前校正网络Gc （s） 具有如下形式的传递函数

从理想的共轭极点中选取s1 ＝－1.50 ＋j2.60， 由原系统开环极点p1 ＝0 到s1 的向量辐角为120°， 由p2 ＝－1 到s1 的向量辐角为100.89°。 根据辐角条件， 超前校正网络提供的辐角应当满足

当k 取为－1 时， 有φ ＝40.89°， 这说明为了使根轨迹经过s1， 我们需要使超前校正网络在s1 处提供辐角φ ＝40.89°。 根据上述条件， 可以有多种确定校正网络参数的方法， 这里使用一种能够尽可能提供较大的α 的方法。 较大的α 有利于减小对系统稳态性能产生的不利影响， 原因在于： 由式（5.79） 可知， 在根轨迹增益确定后， 即在Kc 确定后， 较大的α 能够产生较大的开环增益， 从而产生较大的速度误差系数。

结合图5－33 来说明确定超前校正网络参数的方法。 假设图中点P 所在的位置即为期望的闭环主导极点的位置， 过点P 作平行于虚轴的直线PA， 并连接点P 和原点O。 作直线PB， 使其平分PA 与PO 的夹角。 再作直线PC、 PD， 两者与PB 的夹角分别为－φ／2 和φ／2。直线PC、 PD 与负实轴的交点即为超前校正网络的极点和零点。

图5－33　超前校正网络设计方法

在上述过程中， 令点P 为s1， 并令φ ＝40.89°， 即可得到超前校正网络的零点和极点，它们分别为zc ＝－1.94 以及pc ＝－4.65。 相应地， 有T ＝0.52 以及α ＝0.42。 校正网络传递函数可写为

增益Kc 由根轨迹在s1 处的幅值条件来确定， 即

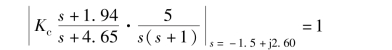
从中解得Kc ＝2.45。 至此， 超前校正网络设计完毕， 其传递函数为

在引入附加开环零、 极点后， 当根轨迹增益K∗＝KcK 由零变化至正无穷时， 根轨迹方程为

绘制出的相应根轨迹， 如图5－34 所示。

从图5－34 中可以看出， 当K∗为12.25， 即Kc ＝2.45 时， 根轨迹恰好与代表ζ ＝0.5 的直线交于s1，2 ＝－1.50 ±j2.60。 此时第三个闭环极点为s3 ＝2.65， 它距离开环零点－1.94 较近， 因此对系统的动态性能影响较小。 由于设计要求中并未对非主导极点作出限制， 因此可以认为设计结果是符合性能指标①的。

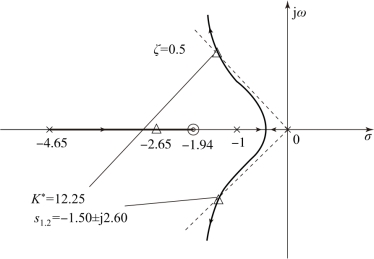
图5－34　例5－14 校正后系统的根轨迹

校正后系统的速度误差系数为

满足设计要求②。

式（5.80） 说明， 使校正网络的零点和极点具有较大的比值， 即选取较大的α 对维持系统的稳态性能具有重要的作用。 但是， 零点和极点具有较大的比值意味着超前校正网络将使原系统的根轨迹向左移动较小的距离， 这不利于动态性能的提升。 从以上分析来看， 稳态性能和动态性能对超前校正网络的要求似乎是矛盾的。

作出的原系统和校正后系统的阶跃响应曲线以及单位斜坡响应曲线， 如图5－35 所示。由图5－35 （a） 可以直观地发现， 超前校正网络为系统的动态性能带来了很大的改善。 由图5－35 （b） 可以发现， 校正后系统的稳态性能与原系统基本一致。

图5－35　例5－14 中原系统和校正后系统的单位阶跃响应曲线和单位斜坡响应曲线

下面给出例5－14 的MATLAB 程序：