参量根轨迹的绘制方法与适用规则

在前面的几节中我们研究了系统在开环增益变化时根轨迹的绘制问题。 在很多情况下，系统的变化参数不为开环增益， 这时所绘制的闭环系统的根轨迹称为参量根轨迹。

在绘制参量根轨迹之前， 首先引入等效单位反馈系统以及等效开环传递函数的概念， 这样， 在对原控制系统作简单处理之后， 常规根轨迹的所有绘制法则均适用于参量根轨迹。 若原系统的闭环特征方程为

［式中， G（s）H（s）包含可变参数］， 那么对式（5.64） 进行处理， 分离可变参数， 得到

式中， A 为系统的可变参数； P（s） 和Q（s） 为与可变参数无关的首一多项式。 根据式（5.65） 可得到图5－23 所示的等效单位反馈系统， 其等效开环传递函数为

图5－23　等效单位反馈系统

由于式（5.65） 与式（5.64） 是等价的， 因此根据开环传递函数式（5.66） 绘制的根轨迹即为可变参数A 产生的根轨迹。 将闭环系统特征方程整理为式（5.65） 的形式后， 便可利用常规根轨迹的绘制法则进行参量根轨迹的绘制。

应当注意， 等效单位反馈系统和等效开环传递函数中的“等效” 二字是针对闭环极点而言的， 而闭环零点一般是不同的， 因此当根据闭环极点和零点分布来分析和估算系统的性能时， 可以采用参数根轨迹上的闭环极点， 但必须采用原系统的闭环零点。

【例5－11】　现有控制系统如图5－24 所示。 试绘制出Kt 由零变化至正无穷时的根轨迹。

图5－24　例5－11 的控制系统

解： 系统的闭环传递函数为

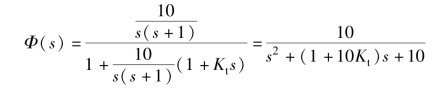
闭环系统的特征方程为

将上式写为

式（5.67） 两侧同时除以s2 ＋s ＋10， 变形为

将式（5.68） 与式（5.65） 对比， 式（5.68） 中的A ＝10Kt， 则等效开环传递函数为(www.xing528.com)

现绘制Kt 由零变化至无穷大， 即A 由零变化至无穷大时的根轨迹。

（1） 确定开环零、 极点。 等效开环传递函数的零、 极点为z1 ＝0， p1 ＝－0.5 ＋j3.12，p2 ＝－0.5－j3.12。

（2） 确定根轨迹分支数以及渐近线。 由于等效开环传递函数m ＝1， n ＝2， 故根轨迹分支数为两条。 根轨迹只有一条与负实轴重合的渐近线， 不必画出。

（3） 确定实轴上的根轨迹。 对于开环零点z1 ＝0 左侧的区间而言， 其右侧实轴上的开环零、 极点个数之和为奇数， 故z1 ＝0 以左的实轴是根轨迹所在的区域。

（4） 确定分离点。 闭环系统的特征方程为

分离点还应当满足

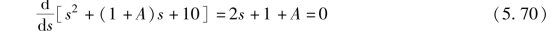
式（5.69） 与式（5.70） 联立， 解得分离点s ＝－3.16， 对应A ＝5.32。

（5） 确定复数极点处的起始角。 对于极点p1 ＝－0.5 ＋j3.12， 有

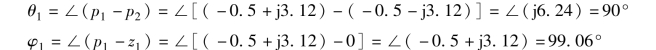
故根轨迹在p1 处的起始角为

根轨迹在p2 处的起始角为

根据上述步骤， 可以绘制出图5－25 所示的根轨迹。

图5－25　例5－11 的参量根轨迹

可以看出， 当闭环系统有一对共轭极点时， 随着Kt 的增大， 闭环系统的阻尼系数不断增大；复平面内的两条根轨迹实际上在以原点为圆心的圆上， 这说明Kt 的变化不会改变闭环系统的无阻尼振荡频率。

下面给出例5－11 的MATLAB 程序：