辐角条件和幅值条件的优化方法

根轨迹是闭环系统所有极点的集合， 在介绍伊文斯提出的根轨迹绘制法则之前， 需要先研究s 平面上的点应满足何种条件才能够成为系统的闭环极点。 假设某控制系统的结构图如图5－3 所示， 现研究其开环增益由零到正无穷变化时的情况。

图5－3 所示的控制系统的闭环传递函数为

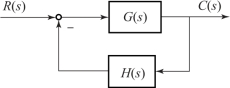
图5－3　某控制系统的结构图

闭环系统的特征方程为

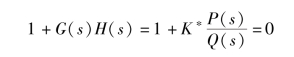
或写为

式（5.4） 中， P（s） 和Q（s） 与可变参数无关， 是关于s 的首一多项式。 记P（s） 和Q（s）的阶次分别为m 和n， 对于一般的物理系统， 有m≤n。 此时， 式（5.4） 等价为

式中， zi 为已知的开环零点； pj 为已知的开环极点（假定所有的开环零、 极点均在左半复平面）； K∗为根轨迹增益， 它由零变化到正无穷。 复平面上满足式（5.5） 的点必然为系统的闭环极点， 故称式（5.5） 为根轨迹方程。

需要注意的是， 为了方便绘制根轨迹， 根轨迹方程中的变化参数为根轨迹增益K∗， 而非开环增益K。 K∗和K 之间仅相差一个比例常数， 下面对两者的关系进行推导。 考虑到可能包含的纯积分环节， 开环传递函数G（s）H（s）可以写为

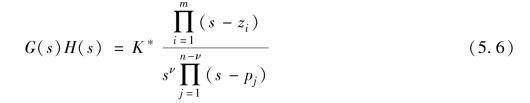
式中， ν 为系统型数。 若将开环传递函数分解为一系列典型环节的基本因子的乘积， 则有(www.xing528.com)

式中， K 为开环增益。 对式（5.6） 进行变换， 有

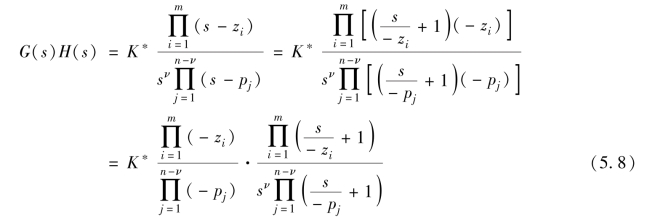
比较式（5.7） 和式（5.8）， 有

以及

式（5.9） 即描述了开环增益与根轨迹增益之间的关系。

应当指出， 只要闭环系统的特征方程可以整理成根轨迹方程， 即式（5.5） 的形式， 无论变化参数是否为开环增益， 均可以绘制根轨迹。 在使用根轨迹方程时， 应当保证方程中开环零、 极点的位置在s 平面上是确定的， 而不是随参数变化而移动的， 否则无法绘制根轨迹。 此外， 当控制系统中变化的参数不止一个时， 绘制出的将不再是简单的根轨迹， 而是根轨迹簇。

再来观察式（5.5） 根轨迹方程式， 由于开环传递函数是关于s 的复变函数， 因此式（5.5） 实际上是一个向量方程， 不方便被我们直接使用。 通过使根轨迹方程左、 右两端的幅值和辐角分别相等， 将其分解为两个方程， 即

式（5.10） 和式（5.12） 分别为根轨迹的幅值条件和辐角条件。 根据这两个条件， 便可以完全确定复平面上的根轨迹以及对应的K∗值。 幅值条件的几何意义： 根轨迹上的某一点所对应的根轨迹增益， 等于所有开环极点到该点的向量模之积与所有开环零点到该点的向量模之积的比值。 辐角条件的几何意义： 所有开环零点到根轨迹上某一点的向量辐角之和与所有开环极点到该点的向量辐角之和的差应当是180°的奇数倍。

辐角条件中未包含K∗， 是确定复平面上根轨迹的充要条件。 也就是说， 可以先使用辐角条件确定复平面上的根轨迹， 再使用幅值条件确定根轨迹上各点的K∗值。 至此， 我们能够在复平面上任取一试探点s1， 通过辐角条件判断其是否在根轨迹上。 若满足辐角条件， 则s1 在根轨迹上， 将其代入式（5.10）， 便可以计算出对应的K∗； 若不满足辐角条件， 则s1不在根轨迹上， 可再选取其他的试探点进行判断。 显然， 这样的试探法仍然是不实用的， 我们需要从辐角条件和幅值条件出发， 进一步研究便于快速绘制根轨迹的法则。