根轨迹的基本概念解析

根轨迹， 又称根迹， 是指控制系统中某一参数的数值从零到无穷大变化时， 闭环系统特征方程的根在s 平面上变化所形成的轨迹。 应用根轨迹曲线研究控制系统特性的方法， 称为根轨迹法。 下面以一个简单的二阶系统为例， 通过解析法来绘制其根轨迹， 进而说明根轨迹的概念以及根轨迹法在控制系统分析与设计中的作用。

【例5－1】　某二阶控制系统的结构图如图5－1 所示， 试绘制其根轨迹图。

图5－1　某二阶控制系统的结构图

解： 根据图5－1 可知该二阶控制系统的闭环传递函数为

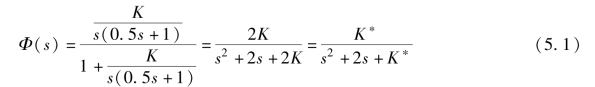
式中， K∗＝2K。 闭环系统的特征方程为

根据一元二次方程求根公式， 式（5. 2） 的解为

观察式（5.3）， 在K 由0 变化至正无穷， 即K∗由0 变化至正无穷的过程中， 当0 ＜K∗＜1 时， 闭环系统有两个负实根； 当K∗＝1 时， 系统在－1 处有一对重根； 当K∗＞1时， 系统有一对实部为－1 的共轭复根。 随着K∗趋于正无穷， 两个根的虚部分别趋于正无穷和负无穷。 综合以上分析， 可以绘制出K∗由零变化至正无穷对应的根轨迹， 如图5－2 所示。 图中粗实线即为根轨迹， 根轨迹上的箭头方向表示特征方程的根随着K∗增大的变化趋势， 图中标注的值即为与该闭环极点位置相对应的K∗值。

(www.xing528.com)

图5－2　例5－1 的根轨迹

根轨迹图直观地反映了控制系统的稳定性、 稳态性能和动态性能。 下面， 我们根据图5－2 对例5－1 中控制系统的上述性能分别进行分析。

1. 稳定性

在开环增益由零变化至正无穷的过程中， 根轨迹没有越过虚轴进入复平面的右半部分，这说明只要在零到正无穷的范围内， 无论开环增益取何值， 系统都是稳定的。 对于其他系统， 根轨迹有可能越过虚轴进入右半平面， 在这种情况下， 称根轨迹与虚轴交点处对应的K值为临界开环增益。

2. 稳态性能

图5－1 所示的系统在原点处有一个开环极点， 因而属于Ⅰ型系统， 由第3章的时域分析可知K 即为静态速度误差系数。 如果给定系统的稳态误差要求， 则由根轨迹图可以确定闭环极点的允许范围。 应当注意的是， 图5－2 中标注的并非开环增益的值， 而是K∗的值，后者称为根轨迹增益。 根轨迹增益和开环增益之间仅相差一个比例常数， 后文将详细介绍两者的关系。

3. 动态性能

从控制系统设计的角度出发， 通过为参数K∗选取特定的值， 我们可以使系统的闭环极点落在根轨迹上的任意位置。 如果根轨迹上的某些极点对应着令人满意的控制系统性能， 我们便可以根据该极点的位置确定K∗， 进而确定系统中待取值的参数； 否则， 我们便需要进一步设计控制器， 改变根轨迹的走向以使其经过代表良好性能的复平面区域。

显然， 对于更高阶次、 更为复杂的系统而言， 使用例5－1 中的解析法来绘制根轨迹是不方便、 不现实的， 我们需要一套能够适用于高阶系统的根轨迹绘制方法。 正是出于这样的目的， 伊文斯提出了具有普适性的根轨迹绘制法则。 需要说明的是， 我们在这里先对变化参数为开环增益， 且变化范围为零到正无穷的常规根轨迹进行研究， 对其他参数发生变化或变化范围为零到负无穷的情况， 我们将其转化为与常规根轨迹相似的问题， 在常规根轨迹绘制法则的基础上稍作修改即可解决。