设计实例：哈勃空间望远镜指向系统的性能优化

【例4－12】　图4－11 所示的哈勃空间望远镜（Hubble Space Telescope， HST） 是以著名天文学家、 美国芝加哥大学天文学博士爱德温·哈勃命名， 在地球轨道上并且环绕地球的太空空间望远镜， 它于1990 年4 月24 日在美国肯尼迪航天中心由“发现者” 号航天飞机成功发射。 它成功弥补了地面观测的不足， 帮助天文学家解决了许多天文学上的基本问题， 使得人类对天文物理有了更多的认识。 此外， 哈勃空间望远镜的超深空视场是天文学家目前能获得的最深入、 最敏锐的太空光学影像。 哈勃空间望远镜指向系统模型如图4－12 所示， 经简化后的结构图如图4－13 所示。

图4－11　哈勃空间望远镜

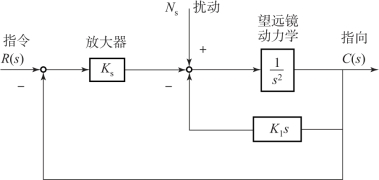
图4－12　哈勃空间望远镜指向系统模型

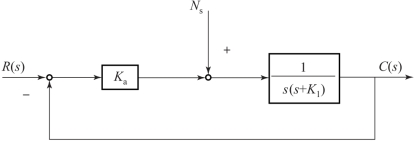
图4－13　哈勃空间望远镜简化结构图

设计目标是选择放大器增益Ka 和具有增益调节的测速反馈系统K1， 使指向系统满足如下性能：

（1） 在阶跃指令r（t） 作用下， 系统输出的超调量小于或等于10%。

（2） 在斜坡输入作用下， 稳态误差较小。

（3） 减小单位阶跃扰动的影响。

解： 由图4－13 可知， 系统开环传递函数为

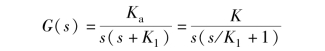
式中， K ＝Ka／K1 为开环增益。

系统在输入与扰动同时作用下的输出为

误差为

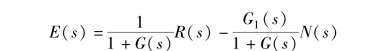
（1） 满足系统对阶跃输入超调量的要求。 令

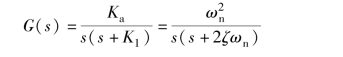
可得(www.xing528.com)

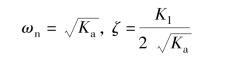
因为

解得

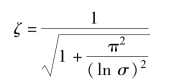
代入σ ＝0.1， 求出ζ ＝0.59， 取ζ ＝0.6。 因此， 在满足σ%≤10%的指标要求下， 应选

（2） 满足斜坡输入作用下稳态误差的要求。 令r （t） ＝Bt， 由表4－1 知

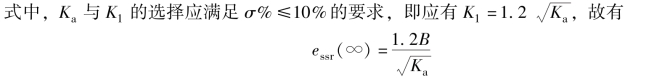
上式表明， Ka 的选取应尽可能大。

（3） 减小单位阶跃扰动的影响。 因为扰动作用下的稳态误差

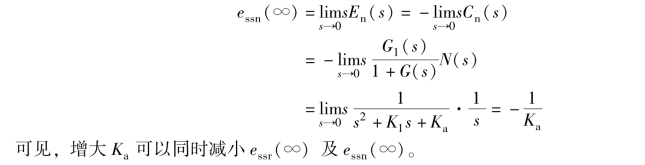
在实际系统中， Ka 的选择必须受到限制， 以使系统工作在线性区。 当取Ka ＝100 时，有K1 ＝12， 此时系统对单位阶跃输入和单位阶跃扰动的响应如图4－14 所示。 可以看出，扰动的影响很小， 且

此时得到了一个很好的系统。

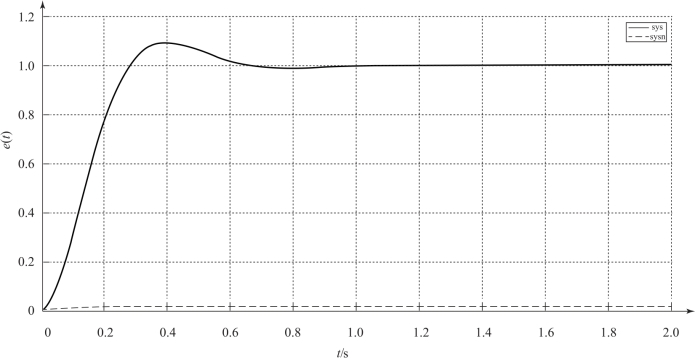
图4－14　单位阶跃输入响应与单位阶跃扰动响应

例4－12 的MATLAB 程序为：