改善机器稳态性能的方法

为了改善系统误差， 工程上一般考虑如下途径。

（1） 系统的实际输出通过反馈环节与输入比较， 因此反馈通道的精度对于减小系统误差起非常重要的作用。 应减小反馈通道中的干扰， 提高反馈通道元件的精度。

（2） 在不影响系统稳定性的前提下， 对于输入引起的误差， 可以通过增大系统开环增益和提高系统型数的方法来减小； 对于干扰引起的误差， 可以通过在系统前向通道干扰点前加积分器和增大放大倍数的方法来减小。

（3） 有的系统要求的性能较高， 既要求系统的稳态误差小， 又对动态性能提出了要求，所以单靠加大开环增益或串入积分环节往往不能同时满足上述要求， 这时可以采用复合控制的方法。 其中补偿的方式可以分为两种情况： 按干扰补偿和按输入补偿。

①按干扰补偿。

当干扰可以直接测得时， 可以利用此干扰进行补偿。 按干扰补偿的系统结构如图4－9所示。

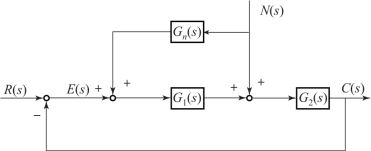
图4－9　按干扰补偿的系统结构

图中Gn（s） 表示补偿器的传递函数， 从而可求出输出对干扰n（t） 的闭环传递函数

若能使这个传递函数为零， 那么干扰对输出的影响就可以消除：

(www.xing528.com)

进而求得对干扰的全补偿的条件为

从系统的结构上看， 这就是双通道原理： 一条通道是由干扰信号经过Gn（s）， G1（s） 到达结构图上的第二个相加点； 另一条通道是干扰信号直接到达此相加点。 两条通道的信号在次点相加， 正好可以互相抵消， 进而实现对干扰的全补偿。

②按输入补偿。

按输入补偿的系统结构如图4－10 所示。 下面将推导确定Gr（s）， 系统满足在输入信号作用时误差得到全补偿。

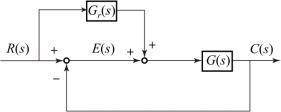
图4－10　按输入补偿的系统结构

单位误差反馈系统

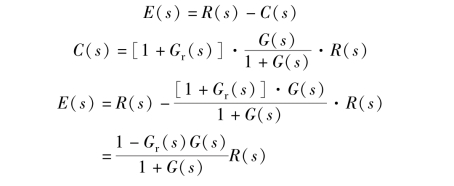
于是有

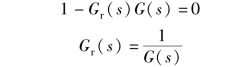
补偿通道并不影响特征方程， 也就是说， 补偿通道不影响系统的稳定性， 因此可以在不加补偿通道的情况下， 调整好系统的动态性能， 以保证有足够的稳定裕量； 再加入补偿通道， 进而只补偿稳态误差、 减小动态误差。 这两种补偿方法已在伺服系统里推广， 在调速系统即加工系统里也有很重要的应用。