斜坡输入下的稳态误差和静态速度误差系数

在图4－3 所示的控制系统中， 若r（t） ＝Rt （其中R 表示斜坡输入函数的斜率）， 则R（s） ＝R／s2。 将R（s） 代入式（4.22）， 得各型系统在斜坡输入作用下的稳态误差为

Ⅰ型单位反馈系统在斜坡输入作用下的稳态误差如图4－7 所示。

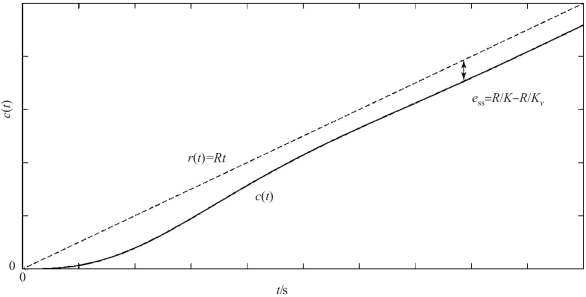
图4－7　Ⅰ型单位反馈系统在斜坡输入作用下的稳态误差

如果用静态速度误差系数表示系统在斜坡输入作用下的稳态误差， 则可将R（s） ＝R／s2代入式（4.22） 得

通常， 式（4.26） 表达的稳态误差称为速度误差。 必须注意， 速度误差的含义并不是指系统稳态输出与输入之间存在速度上的误差， 而是指系统在速度（斜坡） 输入作用下，系统稳态输出与输入之间存在位置上的误差。 容易看出， 0 型系统在稳态时不能跟踪斜坡输入； 对于Ⅰ型单位反馈系统， 稳态输出速度恰好与输入速度相同， 但存在一个稳态位置误差， 其数值与斜坡输入函数的斜率R 成正比， 而与开环增益K 成反比； 对于Ⅱ型及Ⅱ型以上的系统， 稳态时能准确跟踪斜坡输入信号， 不存在位置误差。

如果系统为非单位反馈系统， 其H（s） ＝Kh 为常数， 那么系统输出量的期望值为R′（s） ＝R（s）／Kh， 系统输出端的稳态位置误差为

(www.xing528.com)

式（4.27） 表示的关系对于下面即将讨论的系统在加速度输入作用下的稳态误差计算问题同样成立。

解： 由于系统开环传递函数为

故本例为0 型系统， 其静态位置误差系数Kp ＝K ＝10Kh。 由式（4.22） 可算出系统输入端的稳态位置误差为

系统输出端的稳态位置误差， 可由式（4.23） 算出：

此时， 系统输出量的期望值r（t）／Kh ＝10。