如何定义反馈控制系统的问题误差？

1. 误差与偏差

首先对反馈控制系统的误差信号给出定义。 设某一反馈控制系统结构图如图4－3 所示。其误差有以下两种定义方式。

（1） 从输出端定义的误差一般是指反馈控制系统输出的期望值与实际值之差， 记为E（s）， 则

式中， Cr（s） 是响应输入信号r（t） 的期望输出信号； C（s）是响应输入信号r（t） 的实际输出信号。

（2） 从输入端定义的误差一般是指反馈控制系统的给定输入信号与主反馈信号之差。从系统输入端定义的误差通常称为偏差， 记为ε（s）， 则

偏差和误差之间存在着内在联系。 将图4－3 转换为图4－4 所示的等效形式， 其中， R′（s）即等效单位负反馈系统的输入， 也就是期望的输出， 于是有

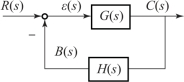
图4－3　反馈控制系统结构图

于是， 图4－4 中E（s） 就是从系统输出端定义的非单位反馈系统的误差， 且满足

根据式（4.9） 和式（4.10）， 可以得到

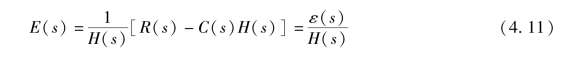
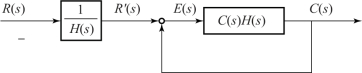
图4－4　等效单位反馈控制系统结构图

实际上， 上述两种误差的定义分别从系统的输出端和输入端直接或间接地体现了系统输出的期望值和实际值之间的差别。 上述两个误差的定义中， 从输入端定义的偏差在工程系统中是可以量测的， 具有一定的物理意义， 而从输出端定义的误差在系统性能指标要求中经常被使用， 但在实际系统中有时无法量测， 因而一般只有数学意义。 在接下来的叙述中， 均采用从输出端定义的误差来进行分析和计算。 需要指出的是， 对单位反馈控制系统来说， 输出量的期望值就是输入信号， 此时两种误差的结果是一致的， 即ε（s） ＝E（s）。

因为误差本身是时间的函数， 其时域表达式为

式中， Φe（s） 为误差传递函数。 对于图4－3 所示的非单位反馈控制系统， 即H（s）≠1 时，满足

由式（4.11） 可得其误差传递函数

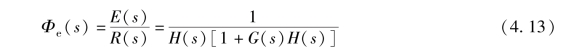
对于单位反馈系统， H（s） ＝1， 则

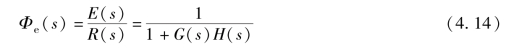
2. 稳态误差定义

由于H（s） 是已知的， 根据式（4.11） 并对其进行拉普拉斯反变换可知， 研究误差信号e（t） 的变化与研究偏差信号ε（t） 的变化是一样的。 因此， 有时只讨论单位反馈系统的稳态误差， 并由此推广到非单位反馈的情况。

如果sE（s） 在s 平面的坐标原点上具有极点， 则sE（s） 并不满足在虚轴上解析的条件。严格说， 此时不能采用终值定理计算稳态误差； 如果使用， 也只能得到无穷大的结果。 问题在于这一无穷大的结果与实际结果相一致， 因此， 从便于使用的观点出发， 把sE（s） 位于原点的极点画到s 平面的左半部内来进行处理。

这是一阶系统， 系统是稳定的。

解法一： 由拉普拉斯变换的终值定理求稳态误差。(www.xing528.com)

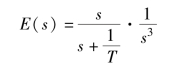
此时， 不符合拉普拉斯终值定理的条件

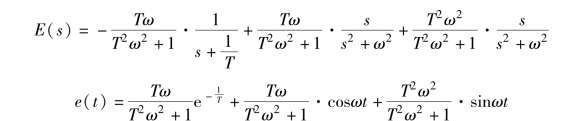
系统的稳态误差为

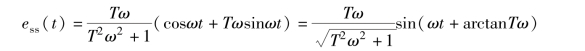
根据上述终值定理的使用条件， 可以说， 如果闭环系统稳定， 且输入信号为阶跃、 速度、 加速度信号或其组合， 则均可用终值定理求稳态误差。

3. 扰动作用下的稳态误差定义

在一个控制系统中， 除了有输入信号输入之外， 还会有各种扰动信号作用。 例如， 负载力矩的变动、 卫星受到的轨道摄动、 电源电压频率的波动、 无人机飞行过程中受到的风力作用等。 因此， 研究扰动信号所引起的稳态误差也具有十分重要的意义。

在理论上， 扰动作用下的稳态误差的分析方法与输入作用下的分析方法相同， 即从理论上将扰动信号看作另一个输入信号。

求给定输入信号作用下的稳态误差的实质问题归结为求误差E（s）。 同理， 求扰动作用下的稳态误差的实质问题归结为求误差En（s）。 设某给定输入信号与扰动信号共同作用下的系统结构图如图4－5 所示。 其中， N（s） 为扰动信号n（t） 的拉普拉斯变换式。

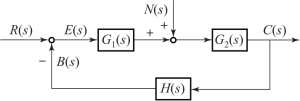
图4－5　给定输入信号与扰动信号共同作用下的系统结构图

为了计算由扰动信号n（t） 引起的系统的稳态误差， 设输入信号r（t） ＝0。 因为在扰动信号N（s） 作用下系统的理想输出应为零， 所以该非单位反馈系统响应扰动信号n（t） 输出端的误差信号为

式中， G（s） ＝G1（s）G2（s）H（s）是非单位反馈系统的开环传递函数； G2（s） 是以n（t） 为输入、 Cn（t） 为输出的非单位反馈的传递函数， 于是， 系统在扰动作用下的误差传递函数为

需要注意的是， 在实际工程系统中， 常常给定输入信号r（t） 和扰动信号n（t） 的作用同时存在。 此时根据叠加原理， 需要把两种信号分别引起的误差或稳态误差叠加在一起。

为了区分两种误差或稳态误差， 用角标r 表示输入信号作用下的误差或稳态误差， 即Er（s） 和essr； 用角标n 表示扰动信号作用下的误差或稳态误差， 即En（s） 和essn。 于是，系统在给定输入信号与扰动信号共同作用下的误差信号为

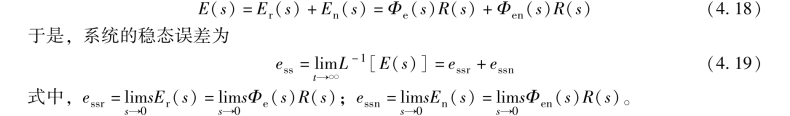
当sEr（s）， sEn（s）在s 平面的右半部（即虚轴上） 解析时， 可以采用终值定理计算系统的稳态误差， 即

【例4－9】　某比例控制系统结构图如图4－6 所示。 设M（t） 为比例控制器的输出转矩， 用以改变被控对象的位置； n（t） ＝1（t）为单位阶跃扰动转矩。 试求系统在扰动作用下的稳态误差。

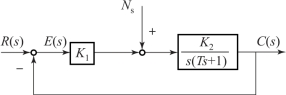
图4－6　某比例控制系统结构图

解： 令R（s） ＝0。 由图4－6 可知， 系统在扰动作用下输出量的实际值为

由于输出的期望值为零， 所以误差信号为

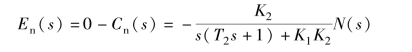
由此可得

则系统在单位阶跃扰动转矩作用下的稳态误差为

本例中， 系统在单位阶跃扰动作用下存在稳态误差的物理意义是明显的。 稳态时， 比例控制器产生一个与扰动转矩大小相等而方向相反的转矩以进行平衡， 该转矩折算到比例控制器输出端的数值为－1／K1， 所以系统必定存在常值稳态误差－1／K1。