稳定性的基本概念与必要条件

任何控制系统在扰动作用下都会产生初始偏差， 偏离原平衡状态。 稳定性是指系统恢复至平衡状态的一种能力。 若系统经扰动后偏离了原来的平衡状态， 且当扰动消失后， 经过足够长的时间， 系统恢复到原来的起始平衡状态， 则称这样的系统是稳定的， 否则， 系统是不稳定的。

为了直观地说明稳定性的概念， 我们以单摆为例。 图4－1 所示为一个单摆， 当无外部扰动作用时， 单摆位于平衡位置a。 假设外部扰动作用在单摆上， 使其偏离平衡点a， 当外部扰动去除时， 由于惯性的作用， 单摆将围绕点a 振荡， 由于空气介质及铰接点摩擦阻力的影响偏摆角将逐渐减小， 经过一定时间后， 摆球又回到平衡点a。 将a 点这样的平衡点称作稳定的平衡点。 而对于平衡点b， 一旦单摆在外部扰动的作用下偏离了该点， 扰动消失后， 无论经过多长时间， 单摆也不可能再回到该平衡点上。 将b 点这样的平衡点称作不稳定的平衡点。

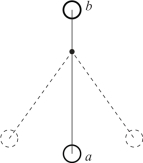
图4－1　单摆

单摆的这种稳定性概念， 可以推广到控制系统的运动状态中。 在研究线性系统的稳定性时， 考察在没有任何外界输入情况下系统方程的解在时间t 趋于无穷时的渐近情况， 显然是要求系统齐次微分方程的解。 由前面的讨论可知， 齐次微分方程的解所含的运动模态与系统的特征根有关， 系统的稳定性由特征根运动模态的敛散性决定。 所以， 线性系统稳定性可以根据系统的特征根在s 平面内的位置予以确定。

即输出增量收敛于原平衡点， 那么线性系统是稳定的。(www.xing528.com)

由于理想单位脉冲δ（t） 的拉普拉斯变换为1， 则系统输出增量的拉普拉斯变换为

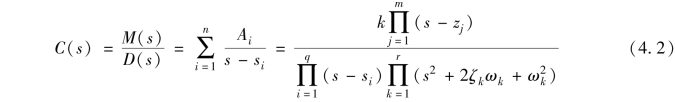
式中， q ＋2r ＝n。 将上式展开成部分分式， 并设0 ＜ζk ＜1， i ＝1，2， … ， r， 可得

由此可见， 线性控制系统稳定的充分必要条件是： 闭环系统特征方程的所有根均具有负实部； 或者说， 闭环系统的极点全部位于s 平面的左半部。

实际上， 稳定性在理论上的一般定义是由俄国学者李雅普诺夫在1892 年率先提出的。除了线性系统， 它对于非线性系统以及时变的、 多变量的各类系统都是适用的。