闭环控制系统的主导极点

在稳定的高阶系统中， 对其时间响应起到主导作用的闭环极点称为闭环主导极点（Closed⁃loop Dominant Pole）。

闭环主导极点具有以下两个特征。

（1） 在s 平面上， 距离虚轴比较近， 且附近没有其他的零点与极点。

（2） 其实部的绝对值比其他极点实部的绝对值小4／5 以上。

由于闭环主导极点距离s 平面的虚轴比较近， 其对应的暂态分量衰减缓慢， 其附近没有零点， 不会构成偶极子， 主导极点对应的暂态分量将具有较大的幅值； 其他的极点具有较大的负实部， 对应的响应分量将较快地衰减为零， 因此， 闭环主导极点主导着系统响应的变化过程。

借助闭环主导极点的概念， 某些高阶系统在一定条件下可被近似为一阶或二阶系统， 以实现对高阶系统的动态性能的评估。 在工程实际应用中， 通常要求系统兼具反应速度和阻尼程度， 因此， 高阶系统常调整增益来使其具有衰减振荡的动态特性。 此时， 闭环主导极点是一对共轭复数， 高阶系统可按二阶系统进行估计。

【例3－4】　已知系统的闭环传递函数为

试估算该系统的动态性能指标。

解： 由闭环传递函数可知， 该系统是一个三阶系统， 其闭环零、 极点在s 平面的分布如图3－14 所示。

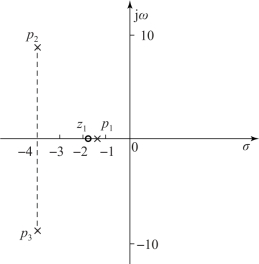
图3－14　零、 极点在s 平面的分布

闭环零点： z1 ＝－1.70。

闭环极点： p1 ＝－1.50， p2，3 ＝－4. 00 ±j9.20。

显然， p1 与z1 构成一对偶极子， 共轭极点p2， p3 是系统的主导极点， 系统可近似为二阶系统， 即

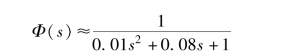(www.xing528.com)

按照二阶传递函数动态性能有

估算动态性能指标为

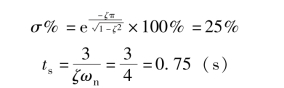
从图3－14 中可以看出， 可以用主导极点对高阶系统动态性能进行近似评估。

【例3－5】　已知闭环传递函数为

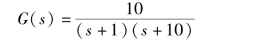
试求系统的阶跃响应。

解：

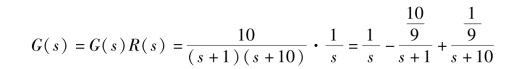
此时， 系统的主导极点是s ＝－1， 系统传递函数近似（降阶后） 为

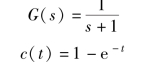
单位阶跃响应曲线如图3－15 所示。 由图可知， 精确曲线与近似曲线只在响应开始时有误差， 且误差越来越小， 并且在3 s 之后逐渐重合， 因此可以用主导极点去实现对高阶系统动态性能的评估。

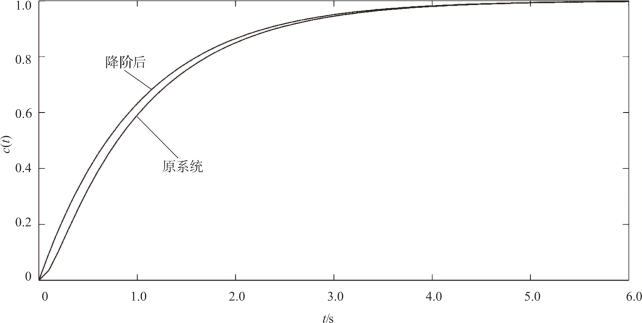
图3－15　单位阶跃响应曲线