二阶系统的脉冲响应特性解析

由于理想单位脉冲函数的拉普拉斯变换为1， 所以系统单位脉冲响应的拉普拉斯变换与其闭环传递函数相同， 故单位脉冲响应具有两重含义： 既是在理想单位脉冲作用下的输出，又是传递函数的原函数。 对于具有标准形式闭环传递函数的二阶系统， 其输出量的拉普拉斯变换为

（1） 当ζ ＝0 时， 二阶系统的响应为欠阻尼响应。 此时， 无阻尼单位脉冲响应为

（2） 当0 ＜ζ ＜1 时， 欠阻尼单位脉冲响应为

（3） 当ζ ＝1 时， 临界阻尼单位脉冲响应为

（4） 当ζ ＞1 时， 过阻尼单位脉冲响应为

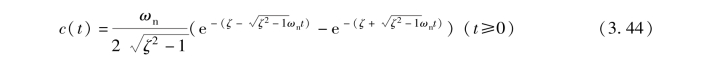
上述各种情况下的脉冲响应如图3－13 所示。

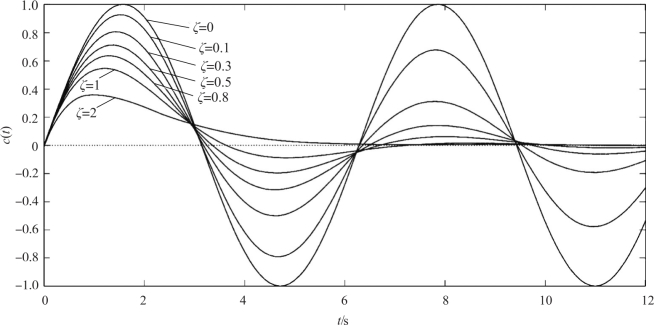
图3－13　二阶系统的脉冲响应与阻尼比的关系

由图可知， 二阶系统的无阻尼脉冲响应是平均值为0 的正、 余弦形式的等幅振荡过程。欠阻尼（0 ＜ζ ＜1） 脉冲响应是稳态值为0 的衰减振荡过程， 其瞬时值有正有负。 而临界阻尼和过阻尼脉冲响应则为单调衰减过程， 且瞬时值不改变符号， 不存在超调现象。

为区分欠阻尼单位脉冲响应与欠阻尼单位阶跃响应， 设c1（t） 为欠阻尼单位阶跃响应，c2（t） 为欠阻尼单位脉冲响应， 其相应的其他性能指标下标也按照此标准区分。(www.xing528.com)

将欠阻尼单位脉冲响应的最大超调量发生的时刻记为tp2， 由

可以求得

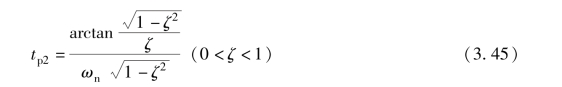
将上式代入式（3.42） 可得脉冲响应的超调量

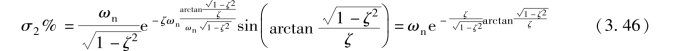
考虑到单位脉冲响应即单位阶跃响应的导数， 可根据二阶系统的单位脉冲响应曲线推导其单位阶跃响应的性能指标。

记t2 为欠阻尼单位脉冲响应c2（t） 第一次过零的时刻， 则有

因此

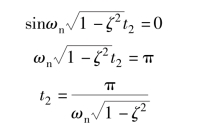
由此可见， 欠阻尼单位脉冲响应第一次过零的时刻t2 与其欠阻尼单位阶跃响应的峰值时间tp1相同。 此时， 对欠阻尼脉冲响应c2（t） 从0 到tp1积分， 有

上式说明， c2（t） 与从0 到tp1的时间轴包围的面积等于1 ＋σ1%， 其中， σ1%为欠阻尼二阶系统的单位阶跃响应超调量。 上述分析说明了欠阻尼二阶系统的单位脉冲响应与单位阶跃响应特征量之间的重要关系。