二阶系统的单位阶跃响应分析

二阶系统的单位阶跃响应的拉普拉斯变换式为

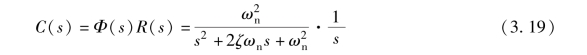
对式（3.19） 取拉普拉斯反变换， 可得二阶系统的单位阶跃响应c（t）。 当阻尼比ζ 不同时，二阶系统的特征根分布不同， 系统的响应也不同。 下面讨论当阻尼比ζ 取值不同时二阶系统的单位阶跃响应。

1. 欠阻尼（0 ＜ζ ＜1） 二阶系统的单位阶跃响应

当0 ＜ζ ＜1 时， 式（3.19） 可以被改写为

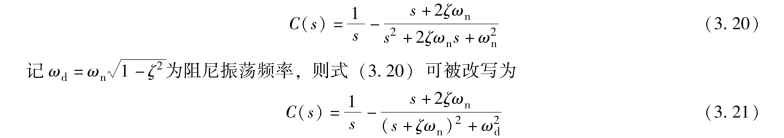
对式（3.21） 取拉普拉斯反变换得

根据式（3.22） 以及式（3.23） 绘制欠阻尼二阶系统的单位阶跃响应曲线及误差曲线， 如图3－8 所示。

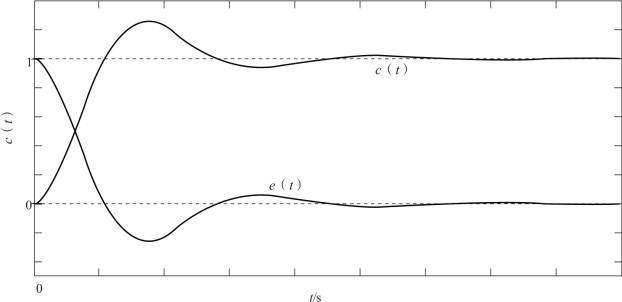
图3－8　欠阻尼二阶系统单位阶跃响应及误差曲线

实际控制系统中通常都存在阻尼比， 因此不可能通过实验方法测得无阻尼振荡频率ωn，而只能测得ωd， 且其值总小于ωn。 只有当阻尼比ζ ＝0 时， ωd ＝ωn。 当阻尼比ζ 增大时，阻尼振荡频率ωd 将减小。 当ζ≥1 时， ωd ＝0， 此时系统输出响应不再出现振荡。

2. 零阻尼（ζ ＝0） 二阶系统的单位阶跃响应

当ζ ＝0 时， 即在无阻尼情况下， 式（3.19） 可以被改写为

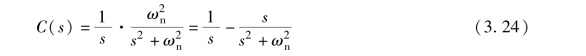
对式（3.24） 取拉普拉斯反变换， 则二阶系统在无阻尼时的单位阶跃响应为

式（3.25） 表明， 二阶系统在无阻尼状态下的单位阶跃响应是一条平均值为1 的正弦（余弦） 曲线， 其振荡频率为ωn， 因此ωn 叫作无阻尼振荡频率。 由于ωn 的取值仅取决于系统本身的结构参数， 是系统的固有频率， 因此也被称为自然频率。(www.xing528.com)

3. 临界阻尼（ζ ＝1） 二阶系统的单位阶跃响应

ζ ＝1 时的阻尼比被称为临界阻尼比。 此时， 式（3.19） 可以被改写为

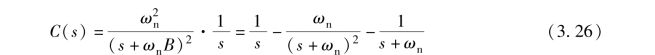
对式（3.26） 取拉普拉斯反变换， 可得二阶系统在临界阻尼时的单位阶跃响应

此时二阶系统的响应称为临界阻尼响应。

显然这是一个不振荡的单调过程， 其稳态值为1， 动态过程也随时间的推移逐渐衰减为零， 指数衰减系数为ωn （又称临界阻尼系数）。 其变换率为

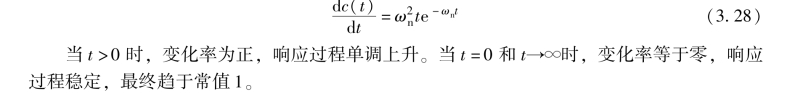
4. 过阻尼（ζ ＞1） 二阶系统的单位阶跃响应

阻尼比ζ ＞1 时被称为过阻尼。 此时， 式（3.19） 可以被改写为

此时二阶系统的响应称为过阻尼响应。

5. 负阻尼（ζ ＜0） 二阶系统的单位阶跃响应

当系统的阻尼比ζ ＜0 时， 称系统处于负阻尼状态， 此时二阶系统的响应称为负阻尼响应。 例如， 当－1 ＜ζ ＜0 时， 二阶系统在负阻尼时的单位阶跃响应为

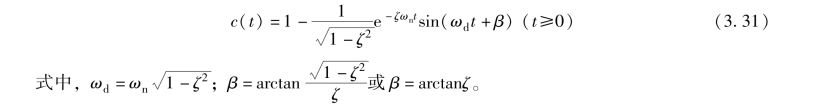
从形式上看， 式（3.31） 与式（3.22） 相同， 但因阻尼比ζ 为负， 所以指数因子e －ζωnt具有正的幂指数， 从而可知此时的单位阶跃响应具有发散正弦振荡的形式。 故二阶系统的负阻尼单位阶跃响应具有发散振荡的形式。

由图3－9 可知， 二阶系统的单位阶跃响应在过阻尼及临界阻尼情况下具有无振荡、 单调上升的特性， 此时二阶系统的单位阶跃响应没有超调量。 从调节时间ts 来看， 在无振荡、单调上升的特性中， 当ζ ＝1 时的ts 最短。 对于欠阻尼响应来说， 单位阶跃响应的振荡特性随着阻尼比的减小而增强， 以至在无阻尼时会出现等幅振荡， 在负阻尼时会出现发散振荡。

由此可见， 阻尼比ζ 对二阶系统的单位阶跃响应的影响非常大。 如图3－9 所示， 在自然频率相同时， 阻尼比越小， 超调量越大， 上升时间越短， 响应越快。 即ζ 越大， 瞬态响应越慢， 系统的快速性越差， 而平稳性增强； ζ 越小， 振荡特性越强， 快速性越强， 平稳性下降。 在实际工程中， 一般要求兼顾平稳性和快速性。 通常希望二阶系统在阻尼比为0.4 ～0.8 的欠阻尼状态工作， 因为在这种状态下， 二阶系统会有振荡特性适度、 调节时间较短的响应过程。