二阶系统的数学模型分析与优化

以二阶微分方程作为运动方程的控制系统， 称为二阶系统。 在控制工程中， 典型二阶系统的应用非常广泛； 除此之外， 还有一系列高阶系统， 它们在一定条件下可以被近似作为二阶系统来研究。 因此， 研究二阶系统的特性具有重要的工程意义。

典型二阶系统的微分方程一般为

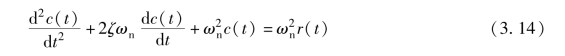
与式（3.13）、 式（3.14） 分别对应的传递函数为

及

现给出典型二阶系统的结构， 如图3－6 所示。

图3－6　典型二阶系统的结构

令式（3.16） 的闭环传递函数的分母多项式为零， 则典型二阶系统的闭环特征方程式为(www.xing528.com)

可得系统的两个闭环极点（特征根） 为

由式（3.18） 可知， ζ 和ωn 这两个参数决定典型二阶系统的时间响应性能。 下面研究二阶系统时间响应及其动态性能指标的求法。 应当注意的是， 对于结果和功用不同的二阶系统，ζ 和ωn 具有不同的物理含义。

根据式（3.18） 可以看出， 典型二阶系统的特征根的性质由阻尼比ζ 的值决定。 二阶系统的特征根分布随阻尼比的变化而变化。 阻尼比取不同值时的特征根分布情况如图3－7所示， 它有如下几种情况：

（7） 当ζ ＝－1 时， 特征方程具有两个相等的正实根s1，2 ＝－ζωn， 其为位于s 平面的正实轴上的相等极点。

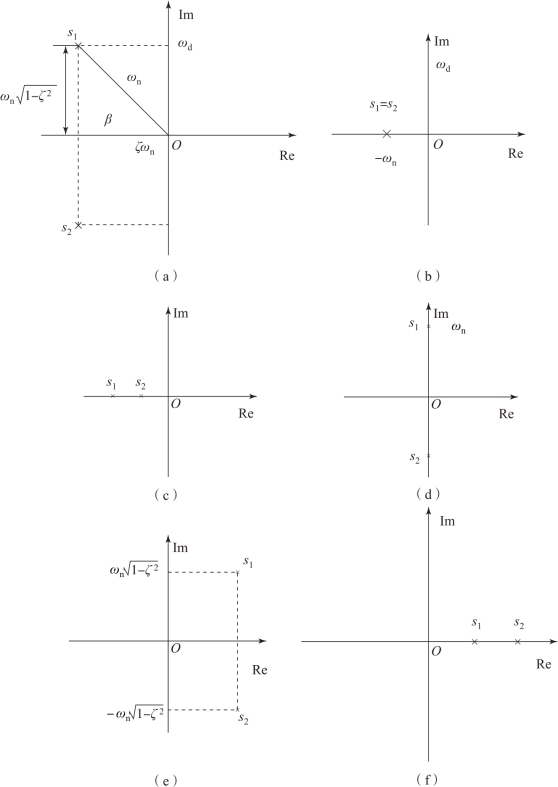
图3－7　二阶系统的闭环极点分布

（a） 0 ＜ζ ＜1； （b） ζ ＝1； （c） ζ ＞1； （d） ζ ＝0； （e）－1 ＜ζ ＜0； （f） ζ ＜－1

接下来， 根据式（3.16） 研究二阶系统的时间响应及动态性能指标的计算方法。