重要传递函数的介绍和应用

反馈控制系统的传递函数， 一般可以由组成系统的元部件运动方程式求得， 但更方便的是由系统的结构图或信号流图求得。 一个典型的反馈控制系统的典型结构图如图2－35 所示。 图中， R（s） 和N（s） 都是施加于系统的外作用， R（s） 是有用输入信号， 简称输入信号； N（s） 是扰动信号； C（s） 是系统的输出信号。 为了研究输入信号对系统输出信号C（s）的影响， 需要求在输入信号R（s） 作用下的闭环传递函数C（s）／R（s）。 同样， 为了研究扰动信号N（s） 对系统输出信号C（s） 的影响， 也需要求取在扰动信号N（s） 作用下的闭环传递函数C（s）／R（s）。 此外， 在控制系统的分析和设计中， 还常用到在输入信号R（s） 或扰动信号N（s） 作用下， 以误差信号E（s） 作为输出量的闭环误差传递函数E（s）／R（s）或E（s）／N（s）。

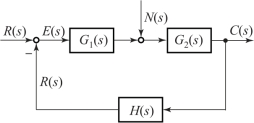
图2－35　反馈控制系统的典型结构图

1. 输入信号作用下的闭环传递函数

应用叠加原理， 令N（s） ＝0， 可直接求出输入信号R（s） 到输出信号C（s） 之间的传递函数为

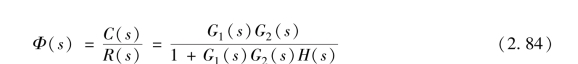
2. 扰动信号作用下的闭环传递函数

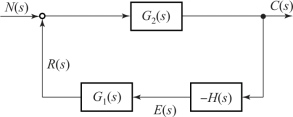
如图2－36 所示， 应用叠加原理， 令R（s） ＝0， 可直接由梅森公式求得扰动信号N（s）到输出信号C（s） 之间的闭环传递函数

(www.xing528.com)

图2－36　在扰动信号作用下的系统结构图

式（2.85） 也可从由图2－35 所示的系统结构图改画成的图2－36 所示的系统结构图求得。 同样， 由此可求得系统在扰动信号作用下的输出

显然， 当输出信号R（s） 和扰动信号N（s） 同时作用时系统的输出为

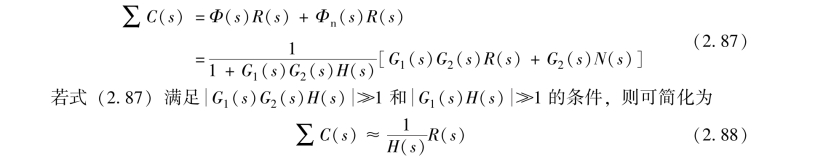
式（2.88） 表明， 在一定条件下， 系统的输出只取决于反馈通路传递函数H（s） 及输入信号R（s）， 既与前向通路传递函数无关， 也不受扰动信号的影响。 尤其是当H（s） ＝1， 即单位反馈时， C（s）≈R（s）， 从而系统近似实现了对输入信号的完全复现， 且对扰动具有较强的抑制能力。

3. 闭环系统的误差传递函数

闭环系统在输入信号和扰动信号作用时， 以误差信号E（s） 作为输入量的传递函数称为误差传递函数。 它们可由梅森增益公式或由图2－35 所示的结构图经等效变换后求得

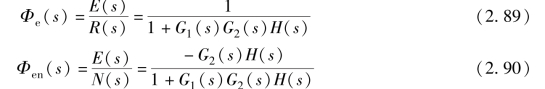
最后要指出的是， 对于典型反馈控制系统， 其各种闭环系统传递函数的分母形式均相同， 这是因为它们都是同一个信号流图的特征式， 即Δ ＝1 ＋G1（s）G2（s）H（s）， 式中，G1（s）G2（s）H（s）是回路增益， 并称它为图2－35 所示系统的开环传递函数， 它等效为主反馈断开时， 从输入信号R（s） 到反馈信号B（s） 之间的传递函数。 此外， 对于图2－35 所示的线性系统， 应用叠加原理可以研究系统在各种情况下的输出量C（s） 或误差量E（s）， 然后进行叠加求出∑C（s） 或∑E（s）。 但绝不允许将各种闭环传递函数进行叠加后求其输出响应。