信号流图的基础知识

结构图虽然可以直观且完整地表示受控变量与输入变量之间的关系， 但对于具有复杂关系的系统而言， 结构图的化简就变得非常复杂且烦琐。 因此， 梅森提出了另一种描述系统变量之间关系的方法： 信号流图法。 信号流图法是将节点和支路组成一种信号传递网络， 利用图示法来描述一个或一组线性代数方程式。 它最大的优点是无须对信号流图进行化简和变换， 直接利用信号流图的增益公式， 给出系统变量间的信号传递关系。 图中节点代表方程式中的变量， 以空心圆圈表示； 支路是连接两个节点的定向线段。 用支路增益表示方程中两个变量的因果关系， 因此支路相当于乘法器。

假如代数方程组为

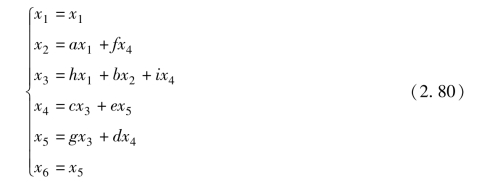
则对应的信号流图如图2－30 所示。

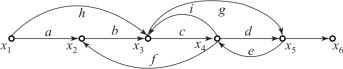
图2－30　式（2.80） 代数方程组对应的信号流图

至此， 信号流图的基本性质可归纳为如下几点。

（1） 节点标志系统的变量。 一般节点按自左向右顺序设置， 每个节点标志的变量是所有流向该节点的信号之代数和， 而从同一节点流向各支路的信号均用该节点的变量表示。

（2） 支路相当于乘法器， 信号在流经支路时被乘以支路增益而变换为另一信号。(www.xing528.com)

（3） 信号在支路上只能沿箭头单向传递， 即只有前因后果的因果关系。

（4） 对于给定的系统， 节点变量的设置是任意的， 因此信号流图不是唯一的。

在信号流图中常使用以下名词术语。

（1） 源节点（或输入节点）： 在源节点上， 只有信号输出的支路（即输出支路）， 而没有信号输入的支路（即输入支路）。 它一般代表系统的输入变量， 故也称为输入节点。图2－30 所示的节点x1 就是源节点。

（2） 阱节点（或输出节点）： 在阱节点上， 只有输入支路而没有输出支路， 它一般代表系统的输出变量， 故也称为输出节点。 图2－30 所示的节点x6 就是阱节点。

（3） 混合节点： 在混合节点上， 既有输入支路又有输出支路。 图2－30 所示的节点x2，x3， x4， x5 就是混合节点。 若从混合节点引出一条具有单位增益的支路， 则可将混合节点变为输出节点， 成为系统的输出变量， 如图2－30 所示的用单位增益支路引出的节点x6。

（4） 前向通路： 信号从输入节点向输出节点传递时， 每个节点只通过一次的通路， 叫作前向通路。 前向通路上各支路增益之乘积， 称为前向通路增益， 一般用pk 表示。 在图2－30 中， 从输入节点x1 到输出节点x6， 一共有四条前向通路： 第一条是x1→x2 →x3 →x4→x5→x6， 其前向通路总增益为p1 ＝abcd； 第二条是x1→x3→x4→x5→x6， 其前向通路总增益为p2 ＝hcd； 第三条是x1 →x2 →x3 →x5 →x6， 其前向通路总增益为p3 ＝abg； 第四条是x1→x3→x5→x6， 其前向通路总增益为p4 ＝hg。

（5） 回路： 起点和终点在同一节点上， 而且信号通过每个节点不多于一次的闭合通路称为单独回路， 简称回路。 回路中所有支路增益之乘积叫回路增益， 用La 表示。 在图2－30中， 从输入节点x1 到输出节点x6， 一共有三个回路： 第一个是起于节点x3， 经过节点x4 最后回到节点x3 的回路， 其回路增益为L1 ＝ci； 第二个是起于节点x4， 经过节点x5 最后回到节点x4 的回路， 其回路增益为L2 ＝de； 第三个是起于节点x2， 经过节点x3， x4 最后回到节点x2 的回路， 其回路增益为L3 ＝bcf。

（6） 不接触回路： 回路之间没有公共节点， 这种回路叫不接触回路。 在信号流图中，可以有两个或两个以上的不接触回路。