传递函数的零点和极点对输出的影响

设某系统的传递函数为

显然， 系统有两个极点： p1 ＝－1 和p2 ＝－2； 有一个零点： z1 ＝－1／3。 系统自由运动模态为e －t和e －2t。 假设输入量为

由拉普拉斯变换， 即

可得系统在零初始条件下的输出象函数

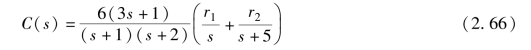
故零初始条件下的响应为(www.xing528.com)

式中， 等式右端的前两项和输入量r（t） 具有相同的模态， 说明它们是由输入量直接产生的强迫运动； 等式右端的后两项包含由极点p1 ＝－1 和p2 ＝－2 引起的自由运动模态， 说明它们是输入量中并不存在的函数类型， 是系统固有的成分， 由系统本身的动态性质决定， 但它们的系数中含有与输入量相关的值r1 和r2， 说明系统的自由运动模态会受到输入量的影响，意味着传递函数的极点会受到输入量的激发， 在输出响应中形成自由运动的模态。传递函数的零点虽然不形成自由运动的模态， 但会影响不同模态在响应中所占的比重，

从而对响应曲线的形状产生影响。 下面将对具有相同极点、 不同零点的传递函数进行比较分析。设传递函数为

两者极点均为p1 ＝－1 和p2 ＝－2， 但G1（s） 的零点是z1 ＝－1／2， G2（s） 的零点是z2 ＝－4／3。 在零初始条件下， 它们的单位阶跃响应分别为

由两者的表达式可以看出， 输出响应均含有e －t和e －2t， 但两者的系数并不相同， 即这两个模态在系统单位阶跃响应中所占的比重是不同的， 它取决于极点之间的距离、 零点与极点之间的距离， 以及零点与原点之间的距离。 两个系统具有相同的极点， 但G1（s） 的零点z1 与G2（s） 的零点z2 相比， z1 更接近原点， 且距两个极点的距离都比较远， 因此与两个极点有关模态所占比重较大的零点z1 作用较为明显。 因此， 尽管两个系统的模态相同， 但由于零点的位置不同， 其单位阶跃响应的形状也有区别， 如图2－19 所示。

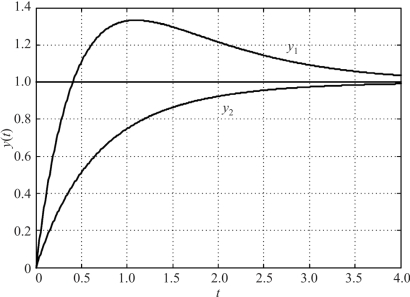
图2－19　零点对动态性质的影响