机械系统中小车的位移运动方程和倒立摆稳定系统的分析

【例2－3】　建立如图2－3 所示的弹簧－阻尼－小车系统的数学模型。

图2－3 所示为弹簧－阻尼－小车系统， 小车的质量分别为m1 和m2， 小车之间由弹簧连接， 希望通过在小车m1 上施加作用力f（t） 来控制小车m2 的位置。 图中连接两辆小车上半部分的为理想弹簧， 理想弹簧产生的力与弹簧两端发生的相对位移成正比， 弹簧的弹性系数为K； 下半部分为阻尼部分， 阻尼力与弹簧两端的相对速度成正比， 比例系数为F。 假设在选择两辆小车位置的参考点时， 弹簧处于自然长度， 则试写出小车m2 在外力f（t） 的作用下位移x2（t） 的运动方程。

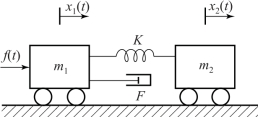
图2－3　弹簧－阻尼－小车系统

解： 系统的输入量为f（t）， 系统的输出量为x2（t）。 由于系统结构较为复杂， 难以直接列写其运动方程， 所以为了简化建模过程， 可选择x1（t） 作为中间变量； 然后根据牛顿第二定律列出方程。

由牛顿第二定律， 左侧的小车满足如下方程：

右侧的小车满足如下方程：

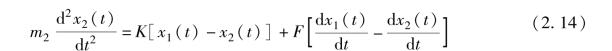
式（2.13） 和式（2.14） 为图2－3 所示的弹簧－阻尼－小车系统的运动方程。【例2－4】　建立如图2－4 所示的倒立摆的数学模型。

倒立摆稳定系统由小车和倒立摆组成， 设M 为小车的质量， m 为摆球的质量， l 为摆长， f（t）为施加在小车上的力。 为了简化问题， 只考虑摆在平面内的运动， 忽略空气阻力及摆杆质量。 系统的输入量是施加在小车上的力f（t）， 输出量是倒立摆与铅垂线的夹角θ。

解： 摆球受力分析如图2－5 所示， 摆球水平方向运动方程为

图2－4　倒立摆

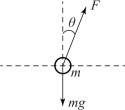
图2－5　摆球受力分析

摆球垂直方向运动方程为

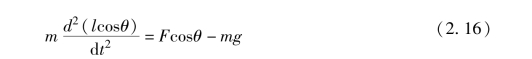
根据图2－6 所示的小车受力分析得其水平运动方程为

(www.xing528.com)

由式（2.17） 可得

将式（2.18） 代入式（2.15） 得

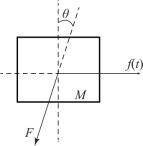
图2－6　小车受力分析

推导可得

整理可得第一个运动方程

由式（2.18） 得

由式（2.20） 和式（2.22） 可得

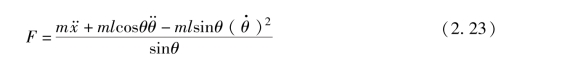
将式（2.23） 代入式（2.16） 得

整理得第二个运动方程为

则该倒立摆系统的运动方程为

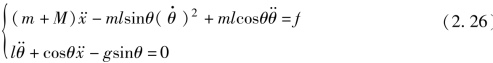
式（2.26） 所示的微分方程组即为倒立摆系统的数学模型。