如何计算机械加/减速时所需电流？

S形加减速的加速度与所采用的设计原则有关，需要根据不同情况，分别计算加减速时的电流有效值。

1.按加速时间、距离及最大速度相同原则设计

根据式（4.4-14），此时，最大加速度a_ms和线性加速最大加速度a_m的关系为

因此，加速转矩、电动机电流也具有和加速度同样的关系，即

代入式（4.5-3），经变换，可得到S形加速时的电流有效值为

对于t₂=0的极限情况，可计算得到各参数值分别为

a_ms=2a_m

I_ms=2I_m

由此可见，为了保持与线性加速相同的加速时间、加速距离及最大速度，进给系统采用S形加速后，驱动器的最大输出电流需要提高到原来的1.155倍。

2.按最大速度、加速度相同原则设计

根据式（4.4-15），此时，最大加速度a_ms、加速时间t_as与线性加速时的最大加速度a_m、加速时间t_a间的关系为(www.xing528.com)

由于a_m相同，电动机加速转矩相同、最大加速电流相等，即

代入式（4.5-3），并经变换，可得到S形加速时的电流有效值为

同样对于t₂=0的极限情况，此时的t_a=t_r，可计算得到各参数值分别为

由此可见，系统采用S形加速后，即使保持与线性加速相同的最大移动速度、最大加速度，其驱动器最大输出电流可减小，在极限情况下，仅需要线性加速的0.577倍。

3.按最大加速度、加速距离相同原则设计

根据式（4.4-16），此时，最大加速度a_ms、加速时间t_as与线性加速时的最大加速度a_m、加速时间t_a间的关系为

同样，由于a_m相同，两种加速方式下的加速电流相等，即I_ms=I_m，代入式（4.5-3），经变换后可得：

对于t₂=0的极限情况，此时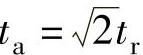，可求得：

由此可见，如果在保持线性加速相同的最大加速度、加减速距离时，采用S形加速将降低最大移动速度、增加加速时间，因此，驱动器最大电流也将减小，在极限情况下，它仅为线性加速的0.577倍。