1.参数确定的方法
一般而言,采用S形加减速的进给系统需要确定的主要参数有加速度变化率限制时间tr、中间加速段时间t2及加速度变化率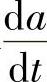 。
。
例如,在FS-0iD上,S形加减速参数如图4.4-3所示,利用CNC参数PRM1620、PRM1621可分别设定图中的T1、tr,其加速段时间t2=T1-tr。
在以上参数中,加速度变化率限制时间tr是最主要的参数。tr一旦确定,其他参数便可根据系统加速区行程Sas、总加速时间tas或最大加速度am的要求,根据式(4.4-12),直接按以下方法计算得到:
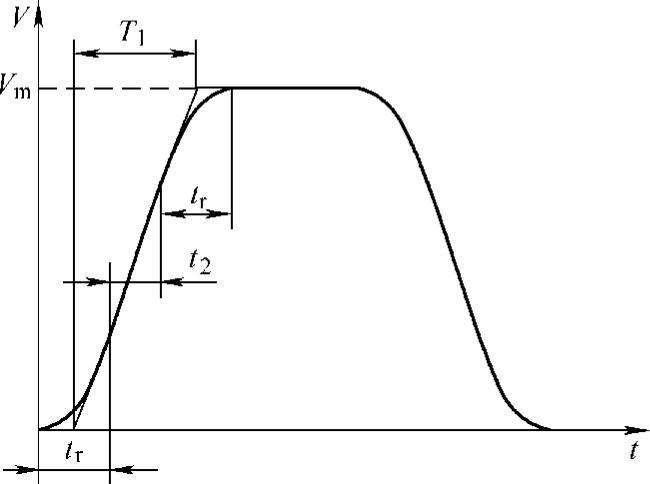
图4.4-3 FS-0iD的参数定义
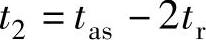
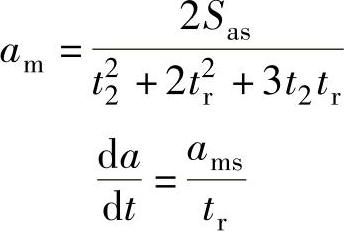
根据经典控制理论,数控机床的伺服进给系统可等效为固有频率为fdmin、阻尼比为ζ的二阶系统,S形加速时的加速度输入可视为上升时间为tr、幅值为ams的斜坡给定输入,系统的动态特性就是二阶系统对斜坡给定输入的响应,因此,速度变化率限制时间tr可按照以下两种方法确定。
2.基于加速度超调的tr确定
根据自动控制理论,二阶系统对斜坡给定输入的动态响应过程及超调量σa%的变化曲线如图4.4-4所示。
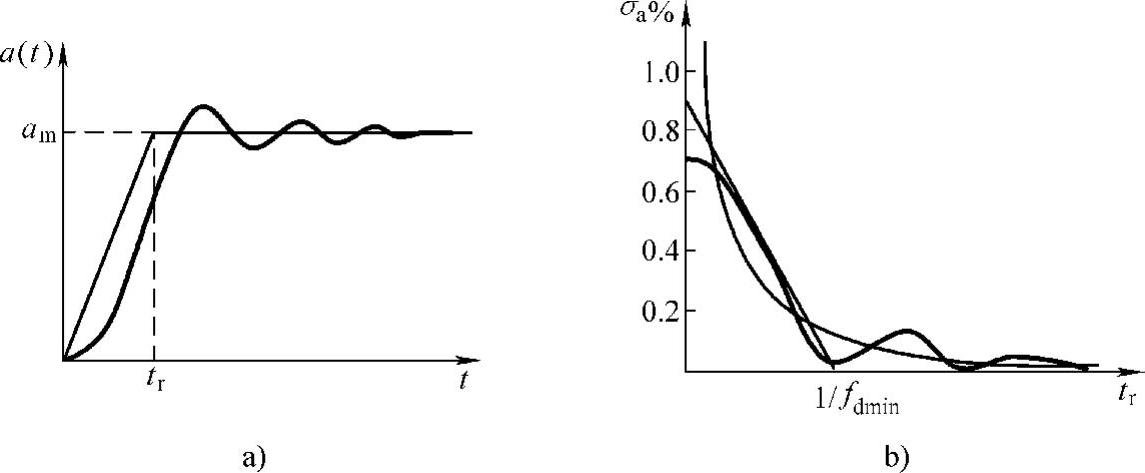
图4.4-4 二阶系统的动态响应
a)响应过程 b)σa%变化
研究表明,在图4.4-4中,当tr<1/fdmin时,加速度超调量σa%随tr的增加而迅速下降,曲线近似直线;在tr≥1/fdmin时,变化渐趋平稳,曲线近似双曲线。因此,在工程计算时,σa%曲线可用如下的分段函数进行近似等效:
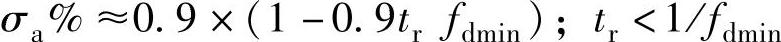
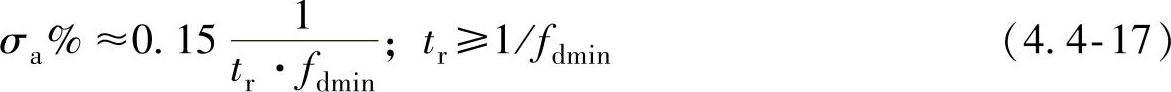
因此,为了有效抑制加速度超调σa%,设计时应仅可能保证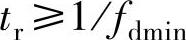 。
。
3.基于位置超调的tr确定
减小加速度超调,实际上也可以减小位置超调,但由于加速度超调不能直接反映位置特性,因此,工程设计一般需要根据位置超调来确定变化率限制时间tr。
根据二阶系统的特点,通过对式(4.4-17)的数学运算处理,可得到tr≥1/fdmin时的位置超调σs%的最大值可由下式近似计算:
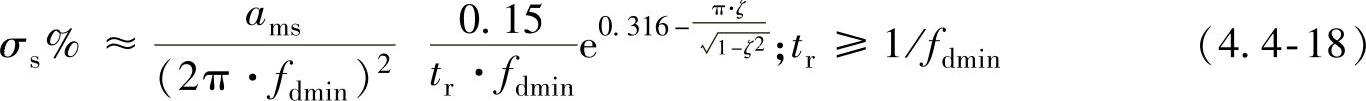
考虑到系统加速度呈线性变化,且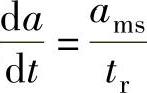 ,上式可简化为
,上式可简化为
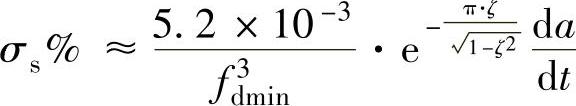
或:
对于特定的阻尼比ζ,可得到如下计算式:
当ζ=0.1时,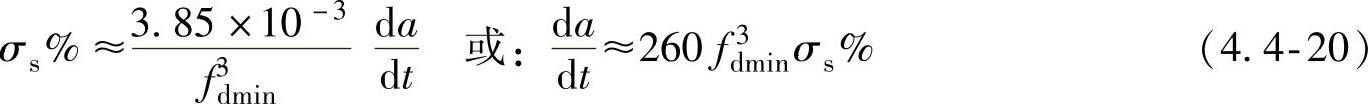
当ζ=0.2时,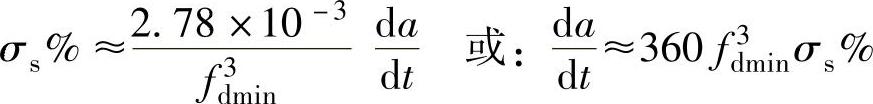 (https://www.xing528.com)
(https://www.xing528.com)
4.参数计算实例
【例9】对于例7,如系统的固有频率为50Hz,ta=0.15s或am=10m/s2保持不变,在考虑加速度超调时,按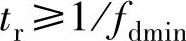 的要求,取tr=30ms;在三种不同的设计原则下,分别可得到如下结论。
的要求,取tr=30ms;在三种不同的设计原则下,分别可得到如下结论。
1)按“加速时间、距离及最大速度相同”原则设计。按这一设计原则,S形加减速必须满足的条件为:
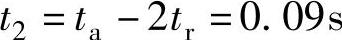
因此,最大加速度ams、最大加速度限制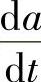
应确定为
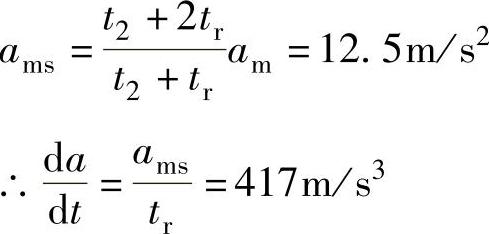
即系统的最大加速度ams需要提高25%,最大移动速度、加速时间、加速行程均与线性加速时相同。
2)按“最大移动速度、最大加速度相同”原则设计。按照这一设计原则,S形加减速必须满足的条件为
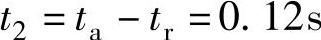 且:
且:
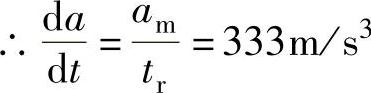
与线性加速相比,采用S形加减速后增加的加速距离ΔSa与加速时间Δta分别为
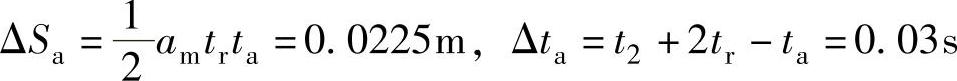
系统的最大移动速度Vm、最大加速度am与线性加速时相同。
3)按“最大加速度、加减速距离相同”原则设计。按照这一设计原则,S形加减速必须满足的条件为
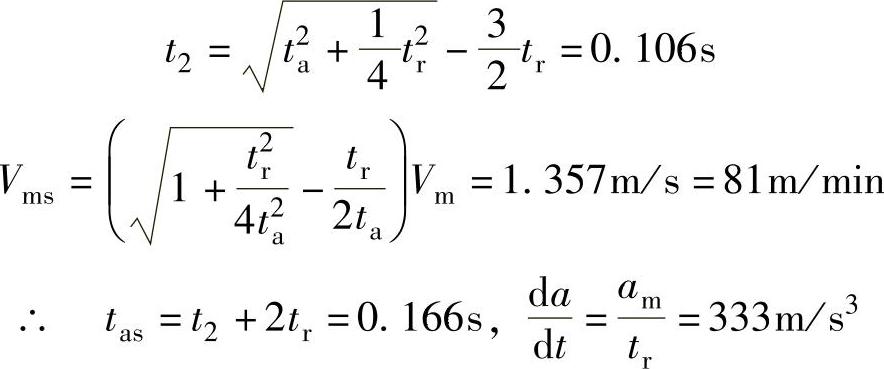
采用S形加减速后,需要降低的最大移动速度ΔVm与增加的加速时间Δta分别为
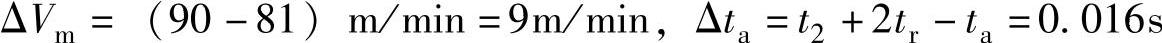
即系统的最大移动速度Vm需要降低10%,加速时间需要增加10%;加速行程、最大加速度与线性加速时的值相同。
【例10】对于例7,若系统的阻尼比ζ=0.1,允许的位置超调为σs%=10μm,如最大加速度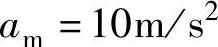 ,
,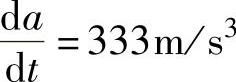 ,其位置超调为
,其位置超调为
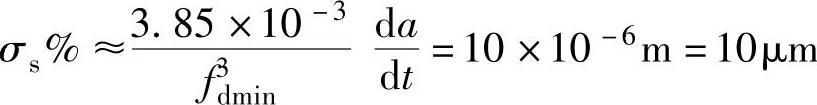
可以满足设计要求。但是,如加速度提高到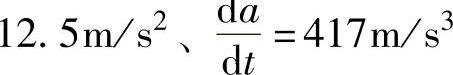 ,其
,其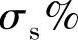 为
为
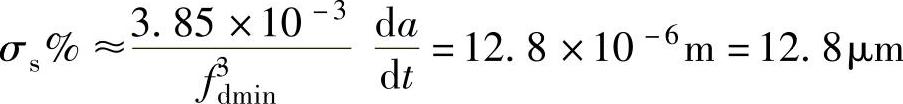
σs%将大于10μm允许范围,故需要根据式(4.4-20)重新计算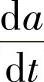 和tr的值。即:
和tr的值。即:
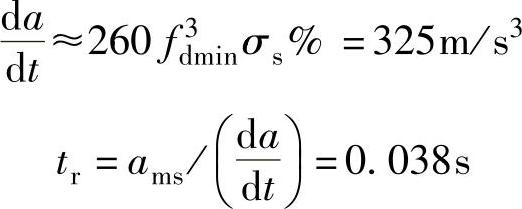
若取tr=40ms.此时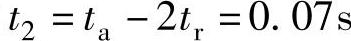 ,系统的最大加速度及相应的位置超调为
,系统的最大加速度及相应的位置超调为
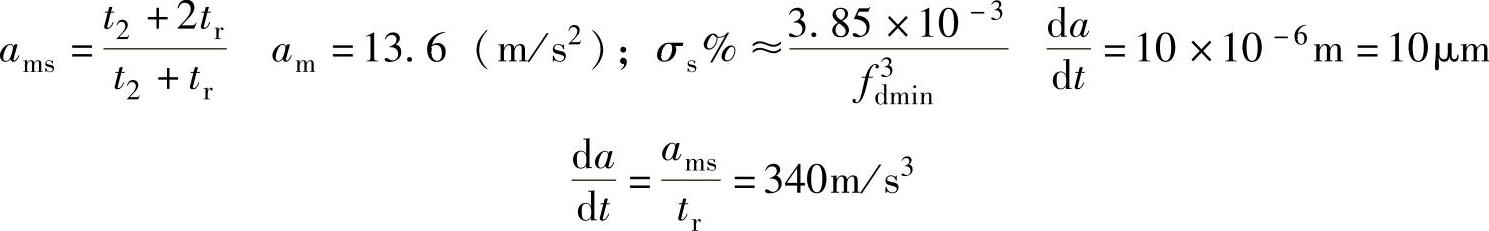
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




