正弦交流电的相量表示法

正弦交流电可用三角函数式（又称为解析式）和波形图表示，三角函数式是基本的表示方法，但运算烦琐；波形图直观、形象，但不准确。为了便于分析计算正弦电路，常用相量（复数）法和相量图表示法表示。后两种方法是分析和计算交流电路常用的方法。它的优点是：第一，把几个同频率的正弦量画在同相量图上，可直观快捷地解决一些特殊的交流电路分析问题；第二，复数运算法准确地解决了复杂交流电路的计算问题。相量表示法的基础是复数，就是用复数来表示正弦量。

1.复数及其四则运算

1）复数

在数学中常用A＝a＋bi表示复数，其中a为实部，b为虚部，称为虚单位电。在电工技术中，为区别于电流的符号，虚单位常用j表示。例如，A＝4＋3j在复平面上的表示如图2－10所示。

在复数坐标平面上，复数A与一个确定的点对应。该点在实数轴（水平轴）和虚数轴（纵轴）上的投影分别为a和b，如图2－11所示。如果用一条带有箭头的有向线段OA把坐标原点和该确定的点A连接起来形成一个矢量，该矢量与复数A对应，称为复数矢量。

图2－10　复数在复平面上

图2－11　复数的矢量表示

复数的代数表示形式为A＝a＋jb。矢量的模和辐角（矢量与实数轴的夹角）为

实部和虚部的计算为

这样，复数就有以下四种表达形式。

复数的代数形式，即

复数的三角形式，即

复数的指数形式，即

复数的极坐标形式，即

实际应用中，代数形式和极坐标形式应用最多，且经常需要将这两种形式进行互相转换。

【例2-8】　写出复数A1＝4－j3，A2＝－3＋j4的极坐标形式。

解：A1的模，辐角θ1＝arctan（－3/4）＝－36.9°，则A1的极坐标形式为A1＝5∠－36.9°。

A2的模，辐角θ2＝arctan（－4/3）＝－126.9°，则A2的极坐标形式为A2＝5∠－126.9°。

2）复数的四则运算

（1）复数的加减法。

设

则

用矢量图表示如图2－12所示。

图2－12　复数相加减矢量图

（2）复数的乘除法。

【例2-9】　求复数A＝8＋j6，B＝6－j8之和A＋B及积A·B。

解：

【例2-10】　试写出1、－1、＋j、－j的极坐标形式并在复平面内画出它们的复数矢量。

解：实数和虚数均可看做复数的特例。

1的极坐标形式为　1＝1∠0°

－1的极坐标形式为　－1＝1∠±180°

＋j的极坐标形式为　＋j＝1∠90°

－j的极坐标形式为　－j＝1∠－90°

在复平面上与之对应的矢量如图2－13所示。

【例2-11】　求复数30∠30°＋40∠－60°。

30∠30°＋40∠－60°在复平面上用矢量的“平行四边形”法则也可求出，如图2－14所示。

图2－13　例2－10图

图2－14　例2－11图

【例2-12】　已知A＝6＋j8，B＝4－j3，求AB和A/B。

解：

2.正弦量的相量表示法

一个正弦量具有幅值、频率及相位3个参数。用三角函数式或波形图来表达正弦量是最基本的表示方法。但是用三角函数式进行电路分析与计算是比较麻烦和困难的。由于在正弦交流电路中一般使用的都是同频正弦量，所以常用下面所述的相量图或相量表达式（复数符号法）来进行分析与计算。

根据各个正弦量的大小和相位关系用初始位置的有向线段画出的若干个相量的图形，称为相量图。实际应用中可不画坐标轴，参考相量画在水平方向。(www.xing528.com)

相量图是能够确切表达正弦量3要素的简捷图示法，如图2－15所示，图中用圆周上的点和中心的连线来描述正弦量。

图2－15　正弦电流的相量表示

直线和X轴形成的角度表示横轴，用来描述相位ωt＋φ角；Y方向的长度描述正弦波瞬时值的大小，正弦量便转换为旋转矢量。

所谓“相量法”就是用有向线段表示正弦量的方法。有向线段的长度等于正弦量的幅值，它与横轴正方向间的夹角等于正弦量的初相位角。电压幅值相量用表示；电流幅值相量用表示。

例如，正弦量i＝Imsin（ωt＋θ）可用表示。此外，工程计算中多用其有效值衡量大小，故只需用有效值相量表示即可，如图2－16所示。

例如，u1＝Um1sin（ωt＋θ1），u2＝Um2sin（ωt＋θ2），若求电压u＝u1＋u2，则可通过构成的平行四边形对角线获得，如图2－17所示。

图2－16　相量表示法图

图2－17　同频率正弦量的相量和

一个正弦量可以用最大值和初相形成的矢量来表示，而矢量又可以用复数来表示，那么正弦电量也可以用复数来表示，其中最大值为复数的模，初相为复数的辐角。

表示正弦量的复数称为相量，对于任意一个正弦量，都能找到一个与之相对应的复数，由于这个复数与一正弦量相对应，把这个复数称作相量。在大写字母上加一个点来表示正弦量的相量。如电流、电压，其最大值相量符号为有效值相量符号为。

需要注意的是，相量只是表示正弦量，不是等于正弦量；只有正弦量才能用相量表示，非正弦量不能用相量表示；只有同频率的正弦量才能画在同一相量图上。

用画相量图的方法可以清楚地表示所讨论各正弦量间的相互关系，也可通过作相量图求得所需结果。在实际使用时由于作图精度的限制，特别是分析复杂电路时还是比较困难的。而相量的数学表达——复数符号法才是分析交流电路的一般方法。

复数的表示形式小结。

代数形式：A＝a＋jb；

三角形式：A＝rcosθ＋jrsinθ；

指数形式：A＝rejθ；

极坐标形式：A＝r∠θ。

【例2-13】　写出下列各正弦量的相量形式，并画出相量图。

解：。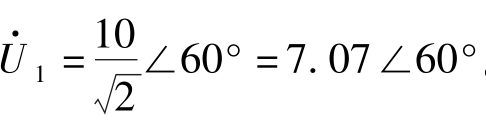

因为u2（t）＝－6sin（100πt＋135°）＝6sin（100πt＋135°－180°）＝6sin（100πt－45°）

u3（t）＝5cos（100πt＋60°）＝5sin（100πt＋60°＋90°）＝5sin（100πt＋150°）

所以

其相量图如图2－18所示。

图2－18　例2－13图

通过以上分析可以知道，一个正弦量由频率（或周期）、幅值（或有效值）和初相位3个要素来确定。正弦量的各种表示方法是分析与计算正弦交流电路的工具。

（1）三角函数表示法也称瞬时值表示法，如

（2）正弦波形图表示法，如图2－15所示。

由于以上两种表达形式对于正弦量进行加、减、乘、除等运算来说是很不方便的，因而还要掌握相量表示法。相量表示法的基础是复数，就是用复数来表示正弦量。

（3）相量图表示法。按照各正弦量的大小和相位关系画出的若干个相量的图形。把几个同频率的正弦量画在同一相量图上，可直观快捷地解决一些特殊的交流电路问题。

（4）复数表示法。分为幅值相量和有效值相量，常用有效值相量如

复数运算法可以十分方便地解决复杂交流电路的计算问题。

相量是一个复数，只是用来表示正弦量，而不等于正弦量，它只是分析和计算交流电路的一种方法。正弦量和相量的相互关系为

交流电路具有用直流电路的概念无法分析和无法理解的物理现象，因此，必须要建立交流特别是相位的概念。因而，任一电压或电流的叠加是矢量和而不是代数和。

另外，还应注意几种量的字母表示形式：瞬时值用小写字母：i、u、e；幅值用大写带下标字母：Im、Um、Em；有效值用大写不带下标字母：I、U、E；相量用大写字母加“·”。

【例2-14】　已知同频率的正弦量的解析式分别为和i＝10sin（ωt＋30°）A，写出电流和电压的相量并绘出相量图。

解：由解析式可得

相量图如图2－19所示，从图中可以看出电流超前电压75°。

图2－19　例2－14图

【例2-15】　已知工频条件下，两正弦量的相量分别为。试求两正弦电压的解析式。

解：由于

【例2-16】　已知，求u1＋u2。

解：将交流电的三角函数式转化为复数的形式，则