电路基本定理详解

1.电阻元件

当电流通过金属导体时，做定向运动的自由电子会与金属中的带电粒子发生碰撞，使导体对电荷的定向运动有阻碍作用。电阻就是反映导体对电流起阻碍作用大小的一个物理量，用字母“R”表示。

在国际单位制中，电阻的单位是欧姆，简称欧，用符号“Ω”表示。其常用单位还有千欧（kΩ）和兆欧（MΩ），它们之间的换算关系为

电阻元件是电路中使用最多的元件之一，常称为电阻器。电阻器的主要特征是变电能为热能，它是一个消耗电功率的元器件，在电路中主要起调节电流、电压及将电能转换成热能的作用。

1）线性电阻元件和非线性电阻元件

电阻元件的特性一般用伏安特性来表示，伏安特性指的是电阻元件两端的电压U与通过其电流I的关系。当电阻器两端的电压与通过它的电流成正比，其伏安特性曲线为线性，这类电阻称为线性电阻器，其电阻值为常数；反之，电阻两端的电压与通过它的电流不是线性关系的电阻称为非线性电阻器，其电阻值不是常数。一般常温下金属电阻器的电阻是线性电阻，在其额定功率内，其伏安特性曲线为直线，如图1－43（a）所示。但像热敏电阻、光敏电阻等，在不同的电压、电流情况下，电阻值不同，伏安特性曲线为非线性，如图1－43（b）所示。

图1－43　电阻器的伏安特性

（a）常温下金属电阻器的线性伏安特性；（b）热敏电阻器的非线性伏安特性

严格地讲，绝对线性的电阻器是不存在的。绝大多数金属导体的电阻都随温度的变化而变化，但这种变化是很小的（除温度特别高以外）可以忽略不计，因此这些电阻器可以看作是线性电阻器。由线性电阻器及其他线性元件组成的电路称为线性电路，含有非线性元件的电路称为非线性电路。

2）电阻的选用

要根据电路和设备的实际要求来选用电阻器，从电气性能到经济价值等方面综合考虑，不要片面地采用高精度和非标准系列电阻器。在一般场合下，主要是根据阻值、额定功率和允许误差的要求来选择合适的电阻器。也就是说，电阻的标称阻值应和电路要求相符，额定功率应该是电阻器在电路中实际消耗的功率的1.5～2倍，允许误差在要求的范围之内。

3）电导

电阻的倒数称为电导，用符号“G”表示，即

导体的电阻越小，电导就越大。电导大就表示导体的导电性能良好，电导的单位是西门子，简称西，用符号“S”表示。

各种材料的导电性能有很大差别。在电工技术中，各种材料按照他们的导电能力，一般可分为导体、绝缘体、半导体和超导体。

（1）导体。

导电能力强的材料称为导体，导体的电阻率一般都约为1×10－8 Ω·m，如铜、铝、铁等金属。

（2）绝缘体。

导电性能很差的材料称为绝缘体。它的电阻率一般为106～108 Ω·m，如橡胶、塑料、树脂、玻璃、云母、陶瓷、变压器油等。

（3）半导体。

半导体的导电性能介于导体和绝缘体之间。半导体的电阻率一般为10－6～106 Ω·m。因为半导体材料具有一些特殊的性质，所以在近代电子技术中得到了广泛的应用。

（4）超导体。

某些物质的电阻随温度的下降而逐渐减少，当温度降低到接近绝对零度（即－273.15℃）时，其电阻突然消失，这种现象称为超导现象。具有这种特性的物质称为超导体或超导材料。

2.欧姆定律

欧姆定律是电路分析中的基本定律之一，是用来确定电路各部分的电压与电流关系的。

1）部分电路欧姆定律

在一段不包括电源的电路中，电路中的电流I与加在这段电路两端的电压U成正比，与这段电路的电阻R成反比，这一结论称为欧姆定律，它揭示了一段电路中电阻、电压和电流三者之间的关系。

图1－44　电阻电路

图1－44所示为电阻电路，标出了电压电流的参考方向，则I、U、R三者之间满足

式中，I为电路中电流（A）；U为电路两端的电压（V）；R为电路的电阻（Ω）。

在交流电路中，欧姆定律同样成立，但电阻应该改成阻抗Z，即

如果已知电压U和电流I，就可以利用R＝U/I求得电阻值。

【例1-10】　有一电灯泡接在220 V的电源上，通过灯丝的电源为0.88 A，求灯丝的热态电阻。

解：根据欧姆定律可得

即灯丝的热态电阻为250 Ω。

【例1-11】　如果人体最小的电阻为800 Ω，已知通过人体的电流为50 mA，就会引起呼吸困难，不能自主摆脱电源，试求安全工作电压。

解：

即人的安全工作电压应不高于40 V。

通常对于不同的人体、不同的场合，安全电压的规定是不相同的。我国有关标准规定12 V、24 V、36 V三个电压等级为安全电压等级。人是否安全与人体电阻大小、触电时间长短、工作环境、人与带电体的接触面积和接触压力等都有关系，所以即使在规定的安全电压下工作，也不可粗心大意。

2）全电路欧姆定律

含有电源的闭合电路称为全电路，图1－45所示为最简单的全电路，图中点画线框部分表示电源，电源内部也有电阻，一般用符号“R0”表示。为了看起来方便，通常可把内电阻R0单独画出，电源内部的电路称为内电路，电源外部的电路称为外电路。

图1－45　最简单的全电路

全电路欧姆定律的内容是：全电路中的电流I与电源的电动势E成正比，与电路的总电阻（外电路的电阻R和内电路的电阻R0之和）成反比，即

式中，E为电源的电动势（V）；R0为电源内阻（Ω）。

由全电路欧姆定律可得E＝IR＋IR0＝U＋IR0，其中U是外电路中的电压降，也是电源两端的电压，称之为路端电压；IR0是电源内部的电压降。

【例1-12】　在图1－45所示电路中，已知电源电动势E＝24 V，内阻R0＝2 Ω，负载电阻R＝10 Ω。

试求：电路中的电流；电源的路端电压；负载电阻R上的电压；电源内阻上的电压。

解：根据全电路欧姆定律，有如下关系式。

（1）电路中的电流为。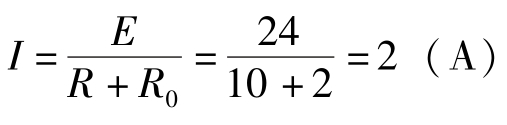

（2）电源的端电压为U＝E－IR0＝24－2×2＝20（V）。

（3）负载R上的电压为U＝IR＝2×10＝20（V）。

（4）电源内阻上的电压为UR0＝IR0＝2×2＝4（V）。

【例1-13】　有一个标有“220 V　25 W”的灯泡，接在220 V的电源上，求通过电灯的电流和灯泡的电阻。如果每晚用4 h，一个月消耗多少电能？（一个月以30天计算）

解　根据公式得

一个月消耗电能为W＝Pt＝25×10－3×4×30＝3（kW·h）

【例1-14】　如图1－46所示电路中，已知E＝6 V，R0＝0.5 Ω，R＝200 Ω，求开关S分别处于1、2、3位置时电压表和电流表的示数。

图1－46　例1－14电路图

解（1）S处于1时，电路呈短路状态，有

（2）S处于2时，电路呈开路状态，有

（3）S处于3时，电路呈通路状态，有

3）电源的外特性

由全电路欧姆定律可得U＝E＝IR0。当负载电阻R为无穷大，即外电路开路，I＝0，两端电压最高且等于E；当负载电阻R变小时，电路中的电流I将增加，内阻压降IR0随着增加，两端电压U将减小。反过来，R增大时，I减小，U将增加。这种电压随负载电流变化的关系称为电源的外特性。所绘成的曲线称为电源的外特性曲线，如图1－47所示。由图1－47可以看出，电源两端电压随着电流的大小而变化，当电路接小电阻时，电流增大，两端电压就下降；当电路接大电阻时，电流减小，两端电压就上升。

电源两端电压的高低不但和负载电阻有密切关系，而且与电源的内阻大小有关。在负载电流不变的情况下，内阻减小，两端电压就上升；内阻增大，两端电压就下降，当内阻为零时，也就是在理想情况下（这时的电源称为理想电源），两端电压不再随电流变化，两端电压等于电动势，如图1－47中的虚线所示。

图1－47　电源的外特性曲线

3.电位的概念及计算

水之所以能够流动是因为有水位差；电荷之所以能够流动是因为有电位差，电位差也称为电压。在电工技术中，通常使用电压的概念，而在电子线路中，通常要用到的是电位的概念。

1）电位的概念

在电路中任选一个参考点（该点的电位值为零，又称为零电位点），电路中某一点到参考点的电压就称为该点的电位。电位的符号用“V”表示，如电路中某点a和参考点O间的电压V为a点的电位，记作Va，电位的单位也是伏特（V）。

由电位的定义可知，电压和电位是密切联系的。电位实际就是电压，只不过电压是指任意两点之间，而电位则是指某一点和参考点之间。电路中任意两点之间的电压即为此两点间的电位差，如a、b之间的电压可记为Uab＝Va－Vb。

根据Va和Vb的大小，Uab有以下三种不同情况。

（1）当Uab＞0 V时，说明a点的电位Va高于b点电位Vb。

（2）当Uab＜0 V时，说明a点的电位Va低于b点电位Vb。

（3）当Uab＝0 V时，说明a和b两点等电位，即Va＝Vb。

引入电位的概念后，电压的方向可以看作是电位降低的方向，因此电压也称为电位降。

2）电位参考点的意义(www.xing528.com)

参考点是计算电位的基准点，电路中各点电位都是针对这个基准点而言的。通常规定参考点的电位为零，因此参考点又称为零电位点，用接地符号“⊥”表示。零电位点（参考点）的选择是任意的，一般在电子线路中常选择很多元件的汇集处，而且常常是将电源的一个极作为参考点；在工程技术中则选择大地、机壳作为参考点，若把电气设备的外壳“接地”，那么外壳的电位就为零。

（1）电位的多值性。

电路中各点的电位值是相对的，它与参考点的选择有关，选择不同的参考点，电路中点电位值的大小和正负也不同。

（2）电压的单一性。

电路中任意两点之间的电压，即电位差是唯一的，与参考点的选择无关。如Uab＝2 V，当选择a点为参考点时，Va＝0 V，Vb＝Va－Uab＝－2 V；当选择b点为参考点时，Vb＝0 V，Va＝Uab＋Vb＝2 V。

【例1-15】　如图1－48所示电路中，已知Uac＝3 V，Uab＝2 V，试分别以a点和c点作为参考点，求b点的电位和b、c两点之间的电压。

图1－48　例1－15的电路图

解：（1）以a点为参考点，则Va＝0 V。

已知Uab＝2 V，即Uab＝Va－Vb＝2 V，则Vb＝Va－2＝0－2＝－2（V）。

已知Uac＝3 V，即Uac＝Va－Vc＝3 V，则Vc＝Va－3＝0－3＝－3（V）。

b、c两点间的电压Ubc＝Vb－Vc＝－2－（－3）＝1（V）。

（2）以c点为参考点，则Vc＝0 V。

已知Uac＝3 V，即Uac＝Va－Vc＝3 V，则Va＝Vc＋3＝3（V）。

已知Uab＝2 V，即Uab＝Va－Vb＝2 V，则Vb＝Va－2＝3－2＝1（V）。

b、c两点间的电压Ubc＝Vb－Vc＝1－0＝1（V）。

由上面的计算可见，参考点为a点时，Vb＝－2 V；参考点为c点时Vb＝1 V。但b和c两点间的电压与参考点的选择无关，始终是Ubc＝1 V。

【例1-16】　如图1－49所示电路中，若以B点为参考点，求A、B、C、D四点的电位VA、VB、VC、VD和C、D两点间的电压UCD。改用D点作参考点，再求VA、VB、VC、VD和C、D两点间的电压UCD。

图1－49　例1－16的电路图

解：以B点为参考点，有

以D点为参考点，有

由上述的计算可以看出，电路中各点的电位与参考点有关，参考点改变电位数值也改变，但电路中任意两点的电压与参考点无关。

4.电阻的串并联连接及等效变换

在电路中，电阻的连接形式是多种多样的，其中最常见的是电阻的串联连接、并联连接和混联连接。

1）电阻串联电路

在电路中，若干个电阻依次连接，中间没有分岔支路的连接方式，称为电阻的串联。图1－50所示为3个电阻R1、R2和R3组成的电阻串联电路。

电阻串联电路具有以下特点：

图1－50　电阻串联电路

（a）三个电阻的串联电路；（b）等效电路

（1）在电阻串联电路中，不论各电阻的数值是否相等，通过各电阻的电流为同一电流，这是判断电阻是否串联的一个重要依据。

（2）根据全电路欧姆定律，电阻串联电路两端的总电压等于各电阻两端分电压之和，电阻串联电路的总电压大于任何一个分电压。

（3）串联电路的总电阻（等效电阻）等于各电阻串联之和，电阻串联电路的总电阻大于任何一个分电阻。

（4）电阻串联电路中，各电阻上的电压与它们的阻值成反比。

上述内容表明：电阻串联时，电阻越大分配到的电压越大，电阻越小分配到的电压越小，这就是电阻串联电路的分压原理。通常把上式又称为电阻串联的分压公式。

（5）电阻串联电路的总功率P等于消耗在各串联电阻上的功率之和，且电阻值大者消耗的功率大。

【例1-17】　图1－50（a）所示电阻串联电路，已知R1＝2 Ω，R2＝4 Ω，U1＝6 V，U＝21 V。求：通过R1、R2、R3的电流I1、I2、I3；R2和R3两端的电压；电阻R3；等效电阻R。

解：（1）根据欧姆定律有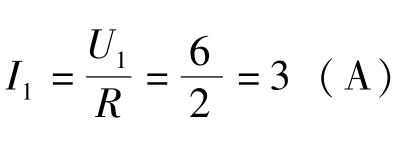；由于是电阻串联电路，所以I1＝I2＝I3＝3 A。

（2）R2两端的电压U2＝I2R2＝3×4＝12（V）；由于U＝U1＋U2＋U3，所以R3两端的电压U3＝U－U1－U2＝3 V。

（3）电阻。

（4）等效电阻R＝R1＋R2＋R3＝7 Ω。

【例1-18】　有个表头电路如图1－51所示，它的满刻度电流Ig为50 μA（即允许通过的最大电流），内阻Rg为3 kΩ。若改装成量程（测量范围）为10 V的电压表，应串入多大的电阻？

图1－51　例1－18图

解：当表头满刻度时，表头两端的电压为

显然用它直接测量10 V电压是不行的，需要串联分压电阻以扩大测量范围（量程）。设量程扩大到10 V所需要串入的电阻为Rb，则

即应串联197 kΩ的电阻，才能把表头改装成量程为10 V的电压表。

2）电阻并联电路

在电路中，将若干个电阻的一端共同连在电路的一点上，把它们的另一端共同连在另一点上，这种连接方式称为电阻的并联。图1－52（a）所示为三个电阻的并联电路，图1－52（b）所示为其等效电路。电阻并联的实例很多，一般家庭中电灯泡的连接方式为并联，即使取下一个灯泡，其他灯泡仍连通着。

图1－52　电阻并联电路

（a）三个电阻的并联电路；（b）等效电路

电阻并联电路具有以下特点：

（1）加在各并联电阻两端的电压为同一电压，电阻两端电压相等。

（2）电路的总电流等于各并联电阻分电流之和，并联电路的总电流大于任何一个分电流。

（3）电路的总电阻（等效电阻）R的倒数等于各电阻的倒数之和，并联电路的总电阻

（4）流过各并联电阻上的电流与其电阻成反比。

上式表明电阻并联时，阻值越大的电阻分配得到的电流越小，阻值越小的电阻分配得到电流越大，这就是并联电阻电路的分流原理。

（5）并联电阻电路的总功率P等于消耗在各并联电阻上的功率之和，且电阻值大者消耗的功率小。

【例1-19】　如图1－53所示，某微安表表头的满刻度电流Ig＝50 μA，内阻Rg＝1 kΩ，若把它改装成量程为10 mA的电流表，问应并联多大的电阻？

图1－53　扩大电流表量程

解：表头满刻度电流只有50 μA，用它直接测量10 mA的电流显然是不行的，必须并联一个电阻进行分流以扩大量程，如图1－53所示，通过分流电阻Rb的电流为

电阻Rb两端的电压Ub与表头两端的电压Ug是相等的，因此有

3）电阻混联电路

在实际应用中，电路里所包含的电阻常常不是单纯的串联或并联，而是既有串联又有并联，电阻的这种连接方式称为电阻的混联。图1－54所示为电阻的混联电路，R1和R2先串联，然后与R3并联，最后与R4串联。

图1－54　电阻的混联电路

求电阻混联电路的等效电路的步骤如下：

（1）先把电阻的混联分解成若干个串联和并联，按照串、并联电路的特点进行计算，分别求出它们的等效电阻。

（2）用已求出的等效电阻去取代电路中的串、并联电阻，得到电阻混联电路的等效电路。

（3）如果所求得的等效电路中仍然包含着电阻的串联或并联，可继续用上面的方法来化简，以求得最简单的等效电路。

（4）利用已化简的等效电路，根据欧姆定律算出通过电路的总电流，再算出各支路上的电流及各电阻两端的电压、功率等。

【例1-20】　如图1－55（a）所示电路，U＝24 V，求等效电阻Rab及电路的总电流I。

图1－55　电阻混联电路的等效电路

解：（1）由图1－55（a）知3 Ω与6 Ω这两个电阻是并联的，其等效电阻为

（2）由图1－55（b）知R′与4 Ω这两个电阻是串联的，其等效电阻为

（3）由图1－55（c）所示电路R″与4 Ω这两个电阻是并联的，其等效电阻为

（4）根据欧姆定律，电路的总电流为

对于较为复杂的电阻混联电路，一般不容易判断出各电阻的串、并联关系，就无法求得等效电阻。遇到这种情况，较为有效的方法就是画出等效电路图，即把原电路图整理为较为直观的串、并联关系的电路图，然后再计算其等效电阻。