C2S转换矩阵稀疏化近似优化

从4.3.1小节对MDCT-MDST转换矩阵的讨论，可以看出N×N的稀疏对角阵T的运算复杂度依旧较高，因此难以在实时要求严苛的移动环境中得到应用。下面再次关注这个稀疏对角阵T。

如果忽略矩阵元素的顺序和符号，式(4.92)稀疏对角阵T的任意行或列的元素组成下式(4.93)序列，容易看出上述序列由两组N/2个不同元素组成，且不相同的元素组成单调递减序列。

定义:矩阵Tm保留(4.92)稀疏对角阵中绝对值最大值的2m个元素值，其他元素均置为0值，即同样忽略矩阵元素的顺序、符号和非0值元素，矩阵T m的任意行或列中组成如下序列，

称上述定义的矩阵T m为稀疏近似化矩阵，即MDCT-MDST转换矩阵T的近似。因此，将(4.91)中T阵用Tm阵替换，第i帧加窗的MDST谱线Yi有如下近似表达式

式中:ind(·)为谱线指标映射函数

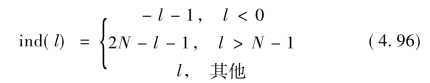
分析上述定义的稀疏化近似矩阵可知:

结论4:MDCT-MDST转换矩阵的运算复杂度从O(N2)下降O(mN)。

下面详细讨论稀疏近似化矩阵Tm与转换矩阵T间的误差。

记B=Tm X+，Bm=T mX+，ΔB=B-Bm，有均方差MSE:

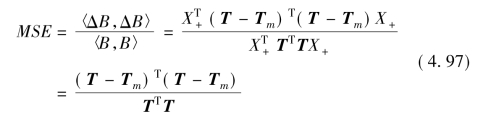
对矩阵S0、S1、C0、C1来说，有性质:

代入式(4.97)的分母，有

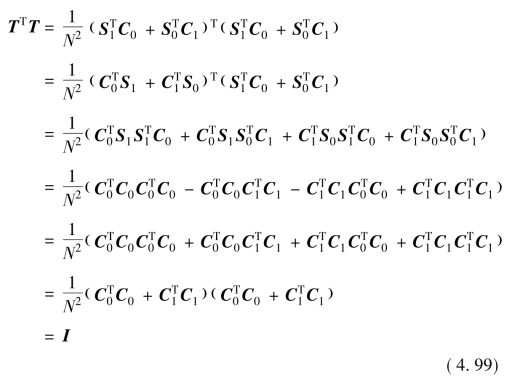(www.xing528.com)

结论5:C2S转换矩阵T是正交矩阵，且其任意列向量的能量和恒定为1。

1.恒等式的发现

进一步考察正交矩阵T，该矩阵的任意列元素如式(4.93)所示，由任意列向量的能量和为1，有

将θ=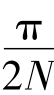代入推导，有恒等式:

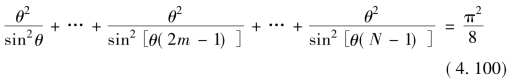
2.均方差的分析

将式(4.99)代入式(4.97)，有

因此，均方差MSE等于矩阵(T-Tm) T( T-Tm)的迹，或者说等于矩阵T-T m所有列向量的能量和。根据矩阵T和T m的定义，将式(4.100)代入，有

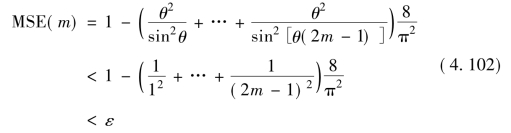
式中:ε为任意小的某值。对于任意给定的ε值，根据上式可获得对应m的取值，于是可知:

结论6:稀疏近似化矩阵T m与矩阵阶数N无关，仅与容许误差ε有关。

3.实例分析

以矩阵阶数N分别为128和1024时的相对误差分析为例，转换矩阵T以T m代替，即它与T在绝对值最大的2mN项相等，其余项为0。对12个不同的音频序列，每个序列取48000点，绘制相对误差随m取值变化的曲线，如图4-12所示。图4-12中，估计值是用公式计算的误差，测试值是根据上述近似方法实际计算得到的误差，由表示相对误差MSE的最大值、平均值和最小值绘制而成。

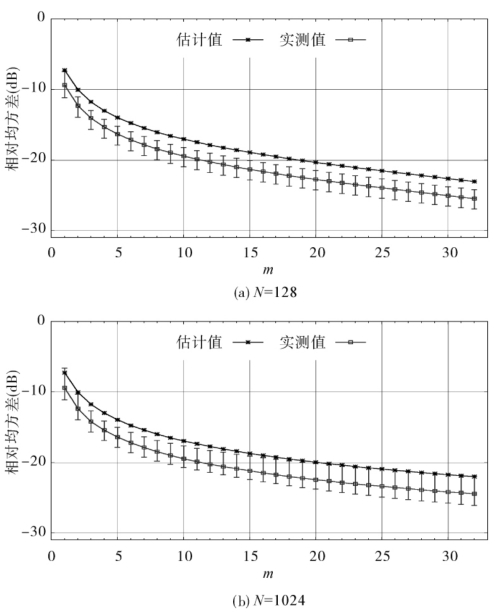
图4-12　D2S相对误差MSE

通过以上分析，例如对任意N，m=2就能满足误差ε=0.1的要求，大大简化了N阶的矩阵操作。因此C2S快速转换方法能极大地降低矩阵运算复杂度。