实验与性能分析探究

为了验证本节所采用的CEM-CWF方法在常用窗形应用中的效果，下面将分别分析正弦窗和KBD窗的DST-IV展开系数，以及CMCLT域下延时相位关系。

1.正弦窗

当指定MDCT变换采用的是正弦窗ws(n)时，相应的MDST采用wc(n)，CMCLT与DFT有简单而有趣的对应关系。

记Yc(k)为第k个MDCT谱线，Xs(k)为第k个MDST谱线，参照(4.70)的定义，通过三角函数积化和差，有

定义¯Zs(k)为Zs+(k)和Zs-(k)组合，有

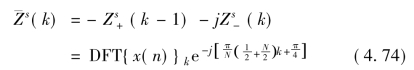
将式(4.74)与(4.71)比较，不难发现前者只是后者的一个特例:正弦窗的DST-IV展开系数除α0=1，其余均为0，此时(4.71)展开式只有第一项l=0有效，于是CMCLT-DFT的转换矩阵V的和展开项仅有一项。因此，以2N为周期信号x(n)，将延时d后信号记为xd(n)，有

式中:表示xd(n)按(4.73)和(4.74)定义得到的谱线。

上面的步骤显示，通过CMCLT实部和虚部的线性组合可以得到一个与DFT仅有相位差的变换，而这个相位差与信号自身无关，保证变换域下提取的声场空间信息能够与输入的时域信号匹配，因此可在实际的空间音频编码系统中应用。正弦窗和余弦窗这一共轭窗在这里起到了关键作用。(https://www.xing528.com)

2.KBD窗

当前音频编码标准(如Dolby AC-3和AAC)除使用正弦窗外，还使用KBD窗(Kaiser-Bessel Derived)。这种窗的形状类似正弦窗，即前半部分单调上升，后半部分单调下降。KBD窗的DST-IV展开系数随频率快速衰减，如图4-9所示。

图4-9　KBD窗的DST-IV变换系数，窗长256，取前128点DST-IV变换

当近似计算时，只需要取前若干项。例如AAC所定义的256点KBD窗，其展开系数前3项分别为α0=0.9801421，α1=-0.1406692和α2=-0.1386815，后面最大的项也只是α2的1/10左右。忽略α3～α127，根据式(4.71)有近似表达式:

式中: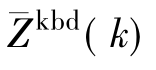，Z k+bd(k)和Z k-bd(k)分别为使用KBD窗及其共轭窗按式(4.73)和式(4.74)定义得到的频谱。

以式(4.76)计算的频谱，其群延时与时域信号的延时具有近似线性对应的关系，这也是式(4.74)的一个近似。例如，对于随机高斯序列及其周期延时信号来说，其相位延时关系非常接近与DFT，如图4-10所示。此时信号的相位就具有了确切的物理意义。

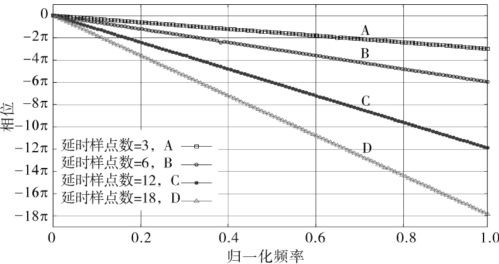
图4-10，时域信号为高斯白噪音

综上所述，本节中提出的CEM-CWF方法，在CMCLT域进行的变换，其频谱不仅能量守恒，而且还可以根据式(4.71)，或其针对正弦窗的简化式(4.74)，或针对KBD窗的近似式(4.76)，得到相位，进而估计信号的延时，求取与延时相位相关的双耳线索，实现高效编码。对于实用的窗函数，其形状多类似于正弦窗或KBD窗，相应的DST-IV频谱主要集中低频。因此，取前若干项近似的方法是普遍适用的。