MDCT频谱对双耳线索的作用分析

4.2.1小节对双耳线索形成机理的分析，考虑了传输过程中的干扰信号，精确的双耳线索计算中需要考虑干扰信号的影响。然而，信源是无法直接观测到的，实际计算时只能依据左右耳入声。因此，当干扰信号足够小时，可以通过如下的时域表达式近似获得双耳线索:

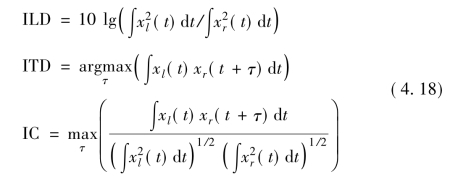
式中:xl(t)和xr(t)分别是左右耳入声。ILD记录了左右耳入声的能量比，ITD记录了具有最大互相关的时间偏移τ，IC记录了此时的归一化相关度。上述积分范围是全时域，对于离散域信号只需将上述积分替换为全时域求和。

值得关注的是，在变换域下为获取与时域保持一致的双耳线索，变换域信号需要满足两个充分条件:第一，变换域信号保持和时域相等的信号能量;第二，时域样点偏移在变换域能够形成线性的附加相位。为此，本文引入MDST解决MDCT域的相位缺失问题，下面将分别考察MDST-MDCT域信号的能量和相位特性，分析新变换域下与时域等价的双耳线索表达式。

MDCT是一种2N点到N点的实变换，相应的逆变换IMDCT为N点到2N点的实变换。其MDCT谱线Xi(k)和IMDCT谱线x'i(n)定义如下:

式中:对音频信号x(n)来说xi(n)是第i帧信号，且

MDST作为MDCT的共轭变换，其谱线Yi(k)和IMDST谱线y'i(n)定义如下:

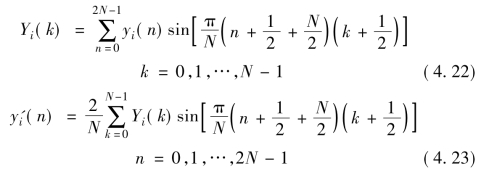
将MDCT谱线Xi(k)看做实部，MDST谱线Yi(k)看做虚部，构造修正离散傅里叶变换(Modified Discrete Fourier Transform，MDFT)，称调制复重叠MCLT变换:

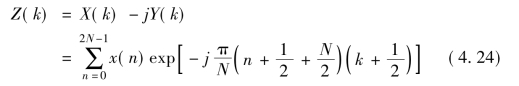
下面首先给出两个基本性质。

性质1:MDCT基函数前半部分奇对称，后半部分偶对称;MDST基函数前半部分偶对称，后半部分奇对称。

从MDCT和MDST的定义可以看到，

MDCT的基函数:

MDST的基函数:

MDCT变换是DCT-IV的变形，增加了N/2的偏移，正是这个偏移项使得MDCT基函数在前半部分n=0，1，…，N-1呈现奇对称，在后半部分n=N，…，2N-1呈现偶对称;MDST在前半部分n=0，1，…，N-1呈现偶对称，在后半部分n=N，…，2N-1呈现奇对称。如错误!未找到引用源。图4-5(a)和(b)分别是MDCT和MDST基函数的奇偶对称示意图。

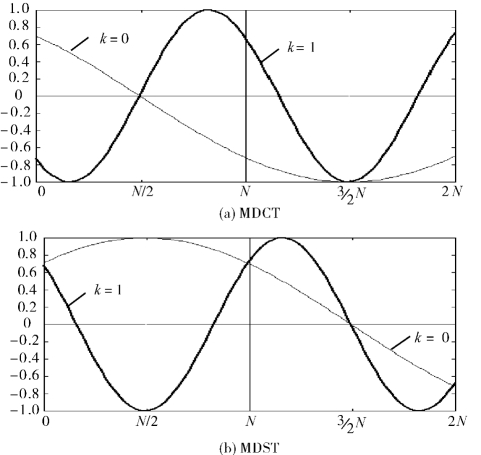
图4-5　基函数的奇偶对称性示意图

性质2:MDCT解码通过重叠区域前后帧相加可以恢复原始信号。

通常单独一次MDCT正反变换不能完全重建原信号，即x'i(n)≠xi(n)。在有50%时域重叠的前后两次MDCT变换中，第i帧的前N点与第i-1帧的后N点处理的是同一时间段的信号，如图4-6所示。

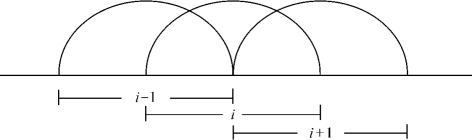
图4-6　MDCT的50%时域重叠示意图

结合图4-5(a)和图4-6，前后两次MDCT的重叠区域对应于同一时间段信号的偶对称分量和奇对称分量，故

1.能量抖动对ILD的影响

在MDCT变换域空间中，当前帧MDCT谱线仅能提供当前帧信号的偶对称分量和下一帧信号的奇对称分量。也就是说，MDCT谱线存在信号能量的抖动现象。在式(4.18)中可以看到双耳线索ILD的时域表达式仅与左右声道信号能量相关，而与最大互相关的时间偏移τ无关。下面我们考察MDCT变换域下的能量抖动对ILD的影响。

MDCT是2N个时域样点到N个频谱样点的实变换，或者说2N维实向量空间到其N维子空间的映射。根据线性空间理论，频域样点的能量在一般情况下不与时域样点的能量相等或只相差一个整系数［118］。下面具体分析MDCT域信号的能量抖动与时域信号能量关系。

记MDCT的N个2N维基向量为ck，MDST的N个2N维基向量为sk，有

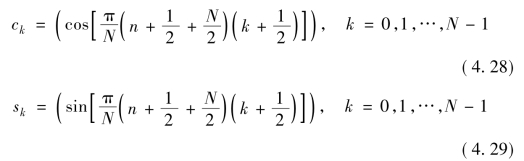
ck之间是相互正交的，sk之间也是相互正交的，故

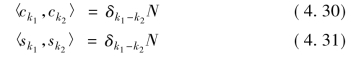
式中:〈*，*〉表示2N维向量空间的内积，δk1-k2是狄拉克(Dirac)符号，当且仅当k1-k2=0时δk1-k2=1，其余情况δk1-k2=0。另外，通过公式(4.28)和(4.29)的三角函数求和，可得ck和sk之间也是相互正交的，即

如果记原2N维空间为Z2N，ck展成的N维空间为CN，sk展成的N维空间为SN，根据线性空间的理论，式(4.28)、(4.29)和(4.30)意味着:

即CN⊥SN且CN∩SN=0，于是ck和sk，k=0，1，…，N-1构成的一组完备正交基，此时有(www.xing528.com)

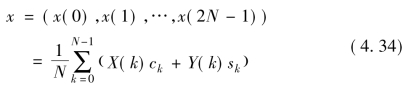
且

上式的左边是时域信号x(n)的能量，右面是其MDCT谱线X(k)和MDST谱线Y(k)或MCLT谱线Z(k)的能量，左右两端仅相差一个常系数。结合式(4.18)，有

结论3:单独的MDCT谱线的能量总是小于时域信号的能量，而MDFT谱线能量是时域信号能量的N倍。双耳线索ILD在变换域的表达式需要使用左右声道信号的MCLT谱线能量比，才能保证与时域表达式等价。

2.延时特性对ITD的影响

从式(4.18)双耳线索ITD的时域表达式可以看到，ITD记录了具有最大互相关的时间偏移τ，而信号的延时特性在MDCT频谱中是没有直接表达的，因此需要对延时的MDCT谱线进行考察。

假设变换长度是2N，信号x(n)有延时d，它记录声波在空气中传输引起的时域延时。对于实际信号，有假设条件

通常情况下，人的双耳间距是不超过0.27m，相应的延时d的范围是±0.8ms，也就是在48kHz采样率下有±38个延时样点。然而，对于MDCT分析窗长2N来说，通常为256或2048个样点，因此假设条件是合理的。也就是说，通常情况下是可以忽略有限求和的边界效应的。为简单起见暂不考虑信号加窗的情况，延时的MDCT谱线

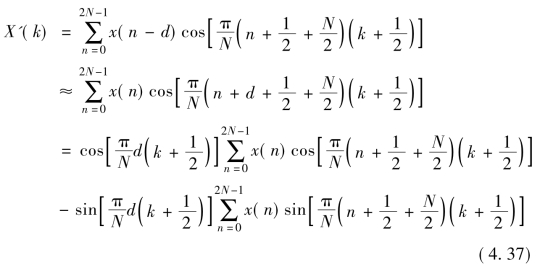
从上式可以看出，延时的MDCT谱线X'(k)不仅依赖于非延时谱线X(k)，还依赖于正弦求和项，即非延时的MDST谱线Y(k)。同理，将MDCT看做实部，MDST看做虚部，有

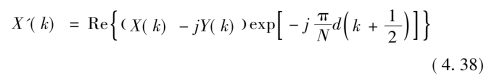
此时我们看到，单一的MDCT延时形成的相位偏移不仅与MDCT频谱相关，还与MDST频谱相关，即时域样点的偏移d在MDCT变换域无法形成线性的附加相位。同理，观察延时的MDST谱线有

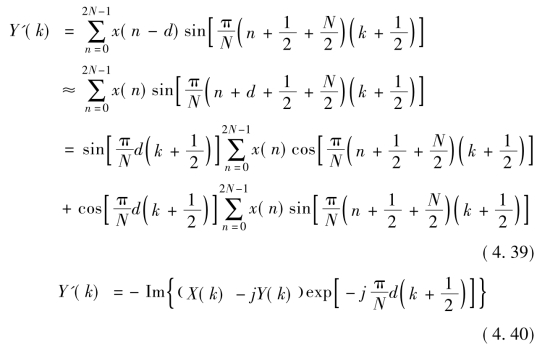
此时我们同样看到，单一的MDST延时形成的相位偏移不仅与MDCT频谱相关，还与MDST频谱相关。也就是说，时域样点的偏移d在MDST变换域也无法形成线性的附加相位。

但是，仔细观察我们发现对于式(4.24)的MCLT变换域的谱线Z(k)来说，结合式(4.38)和(4.40)有

此时，延时的MCLT谱线Z'(k)仅依赖于非延时谱线Z(k)，即时域样点的偏移d在MCLT变换域能够形成线性的附加相位-(π/N)d(k+1/2)。然而此时我们只能说(4.41)是在(4.36)假设条件下的一种近似，在一般情况下是否成立呢?

从延时的MCLT谱线的定义出发，推导信号在MCLT域中的延时相位和时域偏移的关系。与DFT的周期延拓特性x(n+2N)=x(n)类似，为获得MCLT域的线性相位，有条件:

于是

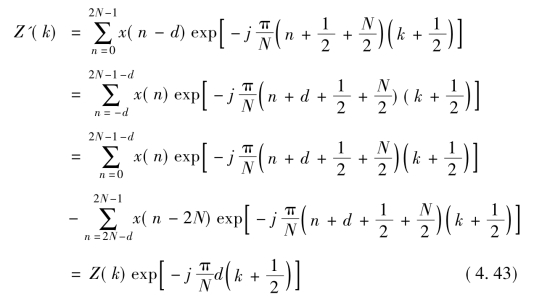
因此，在一般情况下有:

结论4:单独的MDCT谱线延时无法形成线性的附加相位，然而引入MDST形成的MCLT谱线能够在该变换域形成线性附加相位，从而保证双耳线索ITD在变换域的表达式与时域表达式等价，即能够仅通过变换域的相位偏移获得信号的ITD参数。

3.能量延时抖动对IC的影响

从式(4.18)双耳线索IC的时域表达式可以看到，IC记录的归一化相关度不仅与信号的能量有关，而且与最大互相关的时间偏移τ有关。因此需要对延时后的谱线能量进行考察。

根据上面的延时特性分析，延时后的MDCT谱能量和MDST谱能量，有

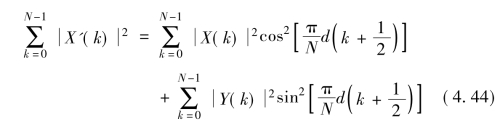
对于单频信号，式(4.41)和式(4.42)意味着能量的周期性变化，如图4-7所示。

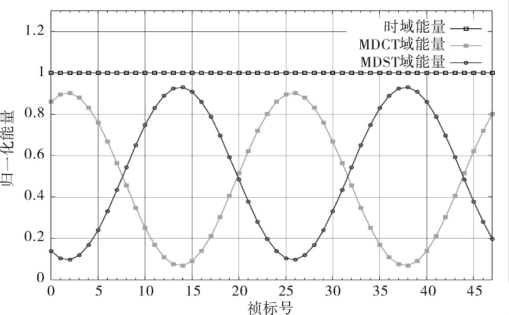
图4-7　 MDCT和MDST能量随延时的周期性编码

信号频率1kHz，N=1024，横坐标延时样点，纵坐标归一化能量

结合式(4.41)和式(4.42)，有

可以看到，等式左侧是延时后MCLT谱线能量，右侧则是时域信号的能量，结合，因此有:

结论5:延时使得MDCT和MDST的频谱能量产生变化，但是它们的能量和保持不变，正好等于时域信号能量。为保证双耳线索IC在变换域的表达式与时域表达式等价，需要采用MCLT谱线来获得信号的IC参数。