双耳线索形成的机理分析

在立体声录制或双耳听音中，从信源出发的声音信号经不同的路径到达集音器或左右耳。声波在传输过程混入噪音的同时也伴随着线性失真和非线性失真。线性失真可视为一种滤波效应，不会产生新的频率分量，而非线性失真受声波传输介质的非线性影响，会产生新的频率分量。对于一般强度的声波来说非线性失真的影响并不显著。

为简单起见，本章只考虑线性失真和干扰音。声源发出的声波经左右路径滤波并叠加干扰音最后到达左右耳，如图4-3所示。

图4-3　传输路径的滤波和噪音作用图

其中，S(t)是声源，hl(t)和hr(t)分别表示左右路径的滤波冲击响应，xl(t)和xr(t)是左右路径接收到的信号，nl(t)和nr(t)表示左右路径的干扰信号，包括噪音和其他声源的信号。相应的左右耳接收信号有表达式为

在空间心理声学理论研究中，hl(t)和hr(t)被称为头相关冲击响应(Head-Related Transfer Impulse Response，HRIR)，用以表明头对声波传输的作用。左右耳的HRIR不仅是时间的函数，同时受到声源偏向角(Azimuth)和高度角(Elevation)等空间位置的影响。根据CIPIC数据库［94］绘制的55°偏向角，0°高度角条件下左右耳HRIR差异曲线，如图4-4所示。

图4-4　左右耳头相关冲击响应差异图

图中可以看出在双耳听音或立体声录音中，左右声道的差异就来自左右耳HRIR差异的影响。因此，在双耳听音中人耳感知的空间参数可视为hl(t)和hr(t)间差异作用的结果，该差异称为头相关差异冲击响应(Head-Related Difference Impulse Response，HRDIR)，用hΔ(t)表示有

式中:表示的逆卷积。

如果将HRDIR仅看做相对延时Δt和衰减Δl的结果，有

式中:δ(t)是单位冲击响应，结合表达式(4.1)、(4.2)、(4.3)有

观察表达式(4.4)，我们发现nr(t)-Δlnl(t-Δt)是具有噪音性质左右路径干扰音的共同作用结果。因此，令r(t)=nr(t)-Δlnl(t-Δt)，代入表达式(4.4)，有

从式(4.5)可以看出，右声道输出信号xr(t)与左声道输出信号xl(t)的强度差为Δl，时间差为Δt，分别对应空间音频编码中的空间参数ILD和ITD，即

结论1:空间音频编码技术中提取的双耳强度差参数ILD是在头相关差异冲击响应的衰减过程中产生的，双耳时间差参数ITD是在头相关差异冲击响应的相对延时过程中产生的。

下面考察双耳相关度IC的形成机理。以下的讨论中均有两点分析推导前提:

(1)延时不影响能量，即

(www.xing528.com)

(2)干扰音nl(t)、nr(t)和声源S(t)两两独立，即

式中:〈·，·〉表示内积。

观察图4-3传输路径的滤波和干扰作用图，记无干扰条件下左耳接收到的信号q(t)=hl(t)*S(t)，左右耳接收信号有关系式:

结合上面所述的两个前提条件，左右耳接收的信号能量有关系式:

此时建立了左右耳接收信号间的内在联系，即右耳接收信号的能量等于左耳接收信号经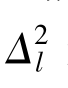衰减后的能量与左路干扰削弱后的能量之和。

将以上左右耳接收信号关系式(4.10)和(4.11)代入xl(t)和xr(t)的互相关函数Rxl，xr(τ)，有

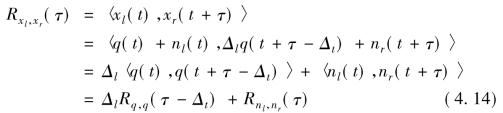
式中:Rnl，nr(τ)是nl(t)和nr(t)的互相关函数，Rq，q(τ-Δt)是q(t)的自相关函数。

将左右耳接收信号的能量关系式(4.12)、(4.13)以及互相关函数式(4.14)代入归一化互相关定义式，有

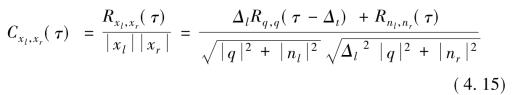
下面我们一起关注两个事实:

(1)nl(t)和nr(t)不相关的前提条件，即Rnl，nr(τ)≡0;

(2)自相关函数在0处取得最大值，该值正是信号的能量。

因此，归一化互相关函数Cxl，xr(τ)的最大值

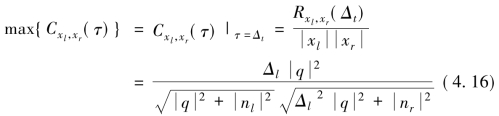
在空间心理声学中max{Cxl，xr(τ)}称为IC，观察等式(4.16)，由于干扰音的存在，右声道输出信号xr(t)与左声道输出xl(t)信号的归一化相关度值函数最大值小于1，即有不等式关系式:

结论2:空间音频编码技术中提取的双耳相关度IC受到干扰音影响而小于1，并且干扰音的相对强度越高反映出的IC越小。

通过以上对双耳线索参数的形成机理分析，我们可以看出:空间音频编码技术中提取的双耳线索参数ILD、ITD和IC都是以原始音频信号为分析提取对象。在基于FFT/CFB/HQMF等变换域的空间音频编码系统中，各空间参数提取公式间是相互等价的，只是表示形式有所差异，我们的目标是在MDCT域中找到一个与它们等价的空间参数表达式。