有效感知量计算单元的计算方法

图3-14所示的空间听觉有限分辨率单元和感知幅度压缩单元是为有效感知量计算服务的。其中，空间听觉有限分辨率单元的输出可采用2.2.2小节中获得的双耳线索ILD、ITD和IC的JND实验结果，分别记为Δτ、Δλ和Δη。但本章实验测试中为简化计算，Δτ、Δλ和Δη采用固定值0.02、1和0.1［109，110］。

根据3.3.1小节的讨论，IC会影响ITD/ILD的感知，但对两者的影响是不同的。当IC减小时，神经兴奋度曲面的延时方向的曲率变化要显著大于衰减方向的曲率变化，在等高线上表现为延时方向变宽明显，而衰减方向变换不明显，如图3-15所示。

2001年Hartmann的实验证实了ILD的恰可感知值在相关噪音下和非相关噪音下仅相差0.5dB［111］。这可以解释为信号的能量与信号的相位无关，IC的降低可以看成相位噪音的增加，因此ILD受IC的影响较小，可忽略不计。

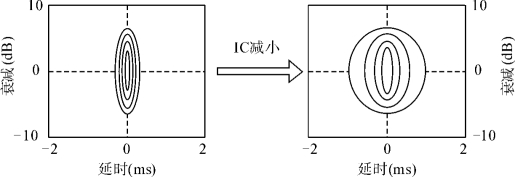
图3-15　IC减小对ITD和ILD的不同影响

然而，信号的互相关曲线的曲率受相关度的影响却很大。以相关噪音为例，其互相关函数是冲击函数，此时曲率趋于无限大，等高线在延时方向退化成一个点，此时可以精确地确定ITD;随着相关度的降低，噪音信号的互相关函数峰值处的曲率逐渐下降，表现为等高线在延时方向扩展，ITD的精度下降;在极端的非相关噪音(即独立噪音)的情况下，互相关函数恒为0，此时等高线由封闭曲线变成延时方向的水平线，完全无法确定ITD。

根据上面的分析，本单元有效感知量q IC计算中忽略IC对ILD的影响，只考虑IC对ITD的影响。由于ITD的分辨率随着IC的下降而下降，相当于ITD的JND增大。因此，本小节计算中假设IC通过影响ITD的JND影响ITD的有效感知量，即(www.xing528.com)

从上式可以看到:当IC(b)=1时，Δτ'(b)有最小值Δτ(b)，此时ITD分辨率最高;当0＜IC(b)＜1时，Δτ(b)＜Δτ'(b)＜∞，此时ITD分辨率下降，但能提供ITD信息;当IC(b)=1时，Δτ'(b)=∞，ITD分辨率为0，无法提供任何ITD信息。因此，ILD、ITD和IC的有效感知量q ILD、q ITD和q IC的计算式如下:

式中:表示下取整。

最后双耳线索的有效感知量进入感知幅度压缩单元，完成空间感知信息的输出。将(3.13)代入(3.8)空间感知熵SPE定义式，有

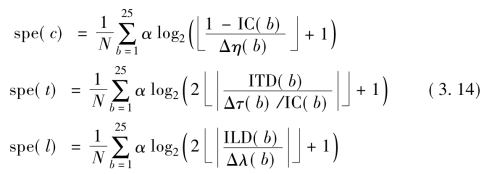
式中:N是FFT变换的帧长，对应于表3-2为1024。ILD(b)、ITD(b)和IC(b)分别由式(3.9)、式(3.10)和式(3.11)给出，Δλ(b)、Δτ(b)和Δη(b)分别是ILD、ITD和IC在临界带b的JND，可通过听音测试确定。α是听觉感知的幅度压缩因子，可通过经验选取，一般取0.6［111］。