常规传输控制能力优化方案

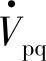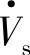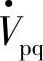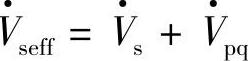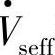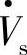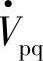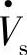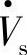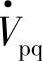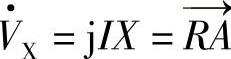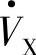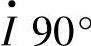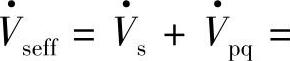
图7-4c给出了UPFC中串联补偿电压实现各种补偿功能时的相量图。首端电压与补偿电压相加得到补偿后线路首端的有效电压，图中超前的相角为ρ，串联补偿电压超前线路首端电压的相位角为ρ，φ₁为超前I·的功率因数角，超前I·的相角为α=ρ+φ₁。线路电压降，超前。。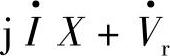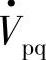是幅值可控、相角可在0～360°范围内可调控的补偿电压，轨迹为以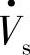相量末端S点为中心、半径为V_pq的圆周，不同相位角ρ的串联补偿电压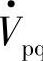具有不同的功能。图7-4中有补偿电压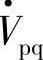时，如果线路首、末端电源电压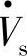、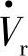之间的相位差为δ，取图中末端电源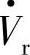相位角零（即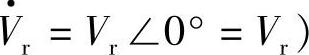，首端电压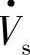超前末端电压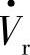相差δ角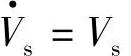，∠δ=V_s e ^jδ，补偿电压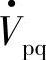超前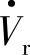的相位角为δ+ρ。

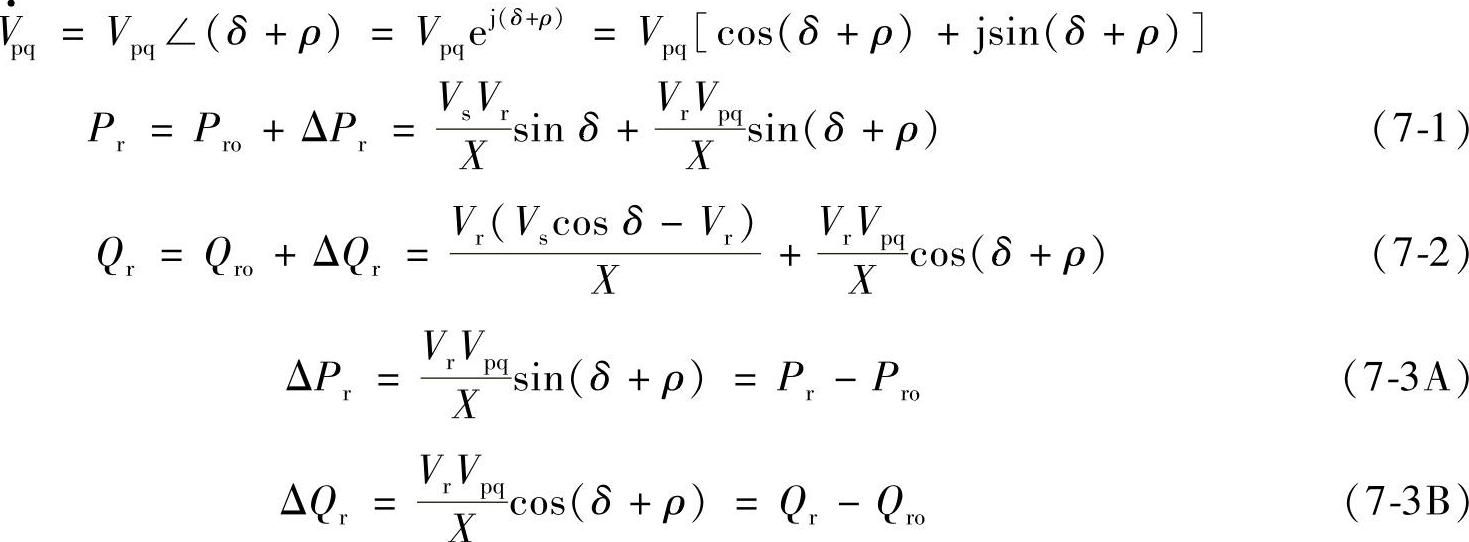
有了补偿电压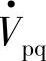以后，线路X首端电压为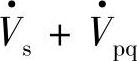，末端电压仍为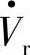，按“叠加原理”图7-4b中的线路末端P_r、Q_r由两部分组成：一是V_pq=0时由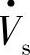、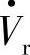（相角差为δ）形成的功率P_ro、Qro；另一部分是V_s=0，由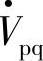、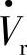（相角差为δ+ρ）形成的ΔP_r、ΔQ_r，由此也可得到式（7-1）、式（7-2）。

如果V_s=V_r=V=V_R（额定电压），在相对单位制中，取电压基值为V_R，功率基值为V²_R/X，阻抗基值为X，则以标幺值表示的功率为

P_r=P_ro+ΔP_r=sin δ+V_pq sin（δ+ρ） （7-4A）

Q_r=Q_ro+^ΔQ_r=（cos δ-1）+V_pq cos（δ+ρ） （7-4B）

-Q_r=（1-cos δ）-V_pq cos（δ+ρ）

ΔP_r=V_pq sin（δ+ρ） （7-4C）

ΔQ_r=V_pq cos（δ+ρ） （7-4D）

P_ro=sin δ （7-4E）

Q_ro=cos δ-1 （7-4F）

当δ+ρ=90°时，可获得最大的ΔP_rmax=V_pqmax；当δ=0°时，可获得ΔQ_rmax=V_pqmax。

若Q_r为正值，则表明首端电源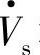和串联补偿电压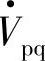经线路X向末端电源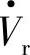注入感性（滞后）无功功率；若Q_r为负值，则表明首端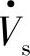和串联补偿电压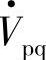经线路向末端电源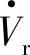注入容性（超前）无功功率。Q_r为负时也表明这时末端电源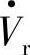向线路输入感性（滞后）无功功率，即三个电压源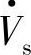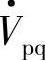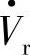（、、）共同承担传输有功功率时线路电抗所消耗的感性（滞后）无功功率I²X。

P_ro、Q_ro是给定功角δ时无补偿系统线路传输的有功功率和无功功率。在给定传输角δ（0≤δ≤π）工作时，由于补偿电压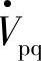的移相角度ρ可在0～2π区间可任意变化，式（7-4C）、式（7-4D）的ΔP_r和ΔQ_r在-V_pq和+V_pq之间独立于δ可控。因此，传输有功功率P_r可控制在最小值P_rmin与最大值P_rmax之间，即

P_rmin=[P_ro（δ）-V_pqmax]≤P_r（δ）≤[P_ro（δ）+V_pqmax]=P_rmax （7-5）

传输的无功功率Q_r可控制在

Q_rmin=[Q_ro（δ）-V_pqmax]≤Q_r（δ）≤[Q_ro（δ）+V_pqmax]=Q_rmax （7-6）

图7-5给出了标幺值V_pq=0.5，在任意传输角δ时线路传输的有功、无功功率可调控的范围。由式（7-4C）、式（7-4D）和图（7-5）可知，无论δ为何值，引入V_pq=0.5后，只要调控补偿电压V_pq的相位角ρ，都可使P_r、Q_r被控量达到ΔP_r=V_pq=0.5，ΔQ_r=V_pq=0.5。线路传输功率的可控部分比较大，且不受传输角δ影响（无论为δ何值，只要ρ=90°-δ，则ΔP≡0.5）。这表明UPFC在潮流控制应用中有其灵活、显著的调控能力，在提高暂态稳定性和减小功率振荡等方面也有很强的能力。

图7-5b中纵坐标为无功功率Q_r，当Q_r值为负时，表明受端电源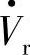向线路输出感性滞后无功。例如无补偿电压V_pq=0时，由于V_s=V_r，在式（7-4F）中，只要传输有功功率，δ≠0，则Q_ro总是为负值，这表明只要传输有功功率P_ro，在V_s=V_r运行工况下，线路首端必须向V_r输送容性无功，或者说受端电源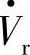必须向线路输出感性滞后无功功率，且P、δ越大，Q_ro^也应越小，即受端电源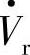也应向线路输出更多的感性滞后无功功率，供线路电抗无功损耗I²X才能使V_r=V_s。

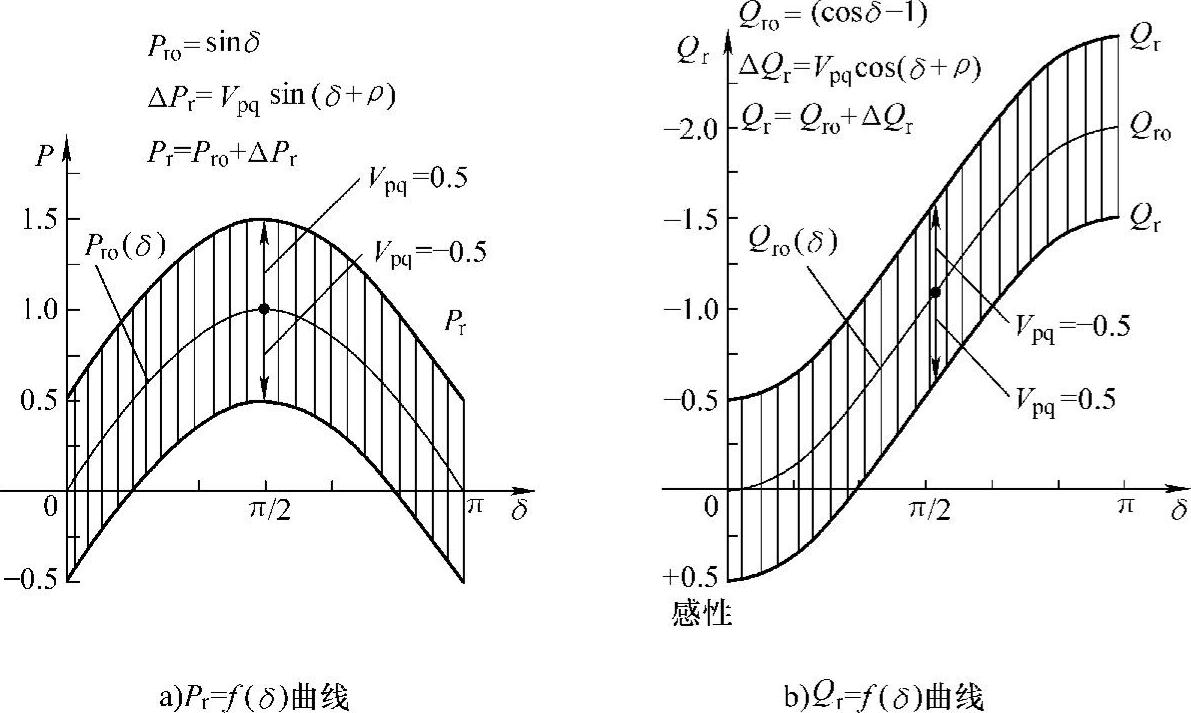
图7-5 UPFC控制的输电线可传输的有功P_r及其受电端无功Q_r与传输角δ的关系

在图7-6a中，假设δ=30°，标幺值V_pqmax=0.5。补偿电压相量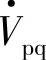，线路首端有效电压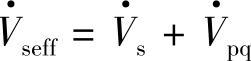。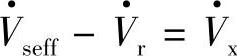是补偿后线路电抗X上的电压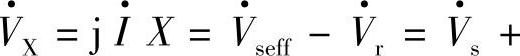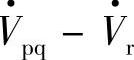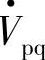，。决定了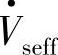的幅值和相位角，也就调节了相量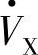的幅值和相角，改变了线路电流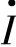的幅值和相位，线路传输功率P_r、Q_r按式（7-4A）、式（7-4B）随V_pq和相角ρ变化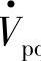，使传输功率的增量ΔP_r、ΔQ_r都与V_pq成正比，并都随移相角δ+ρ变化。

图7-6a中δ=30°，V_pq=0时，P_ro=sin δ=sin30°=0.5，Q_ro=（cos δ-1）=-0.134。线路加入串联补偿电压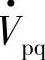以后，传输线首端功率P_s、Q_s可由下式得到：

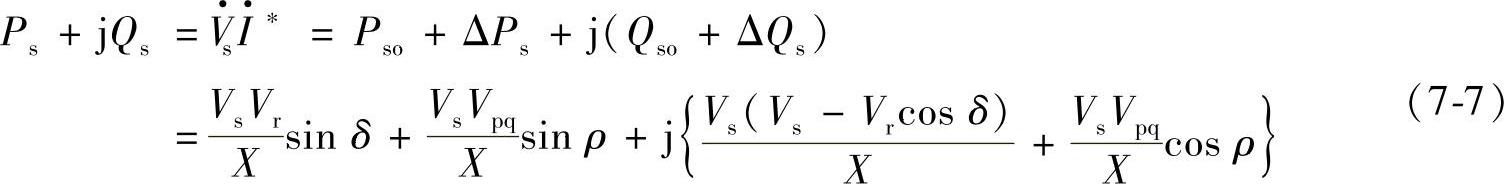
若V_r=V_s=V=V_R，用相对单位表示时，由式（7-7）可得到

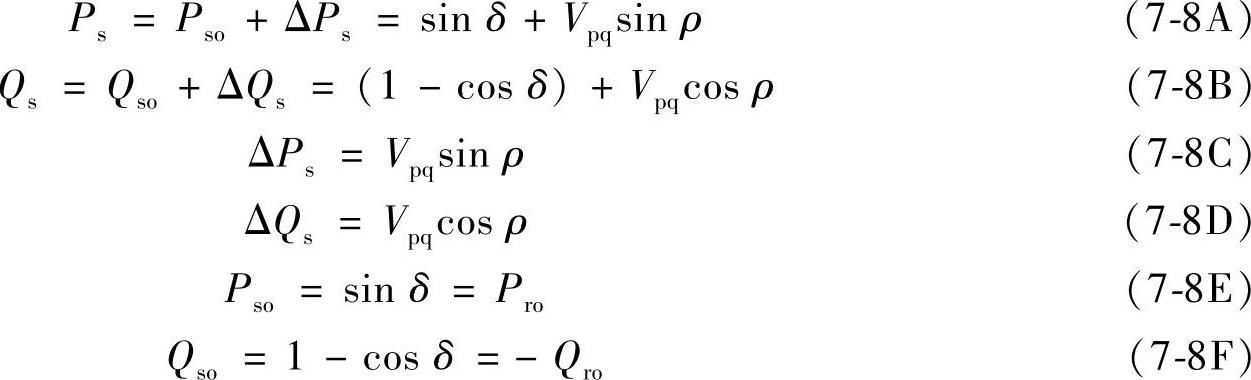
变流器串联注入电压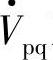对应的串联注入功率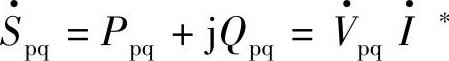，电流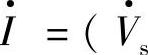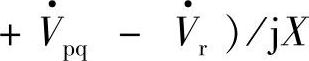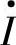，的共轭相量为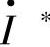，则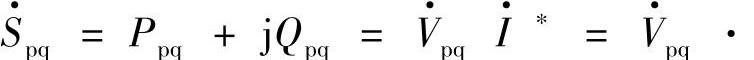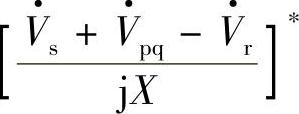，由此可得到

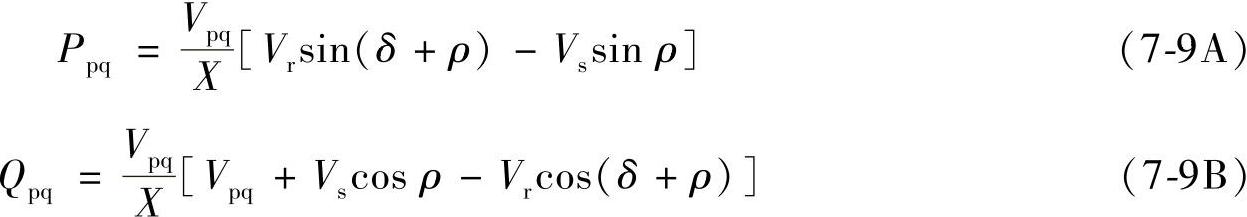
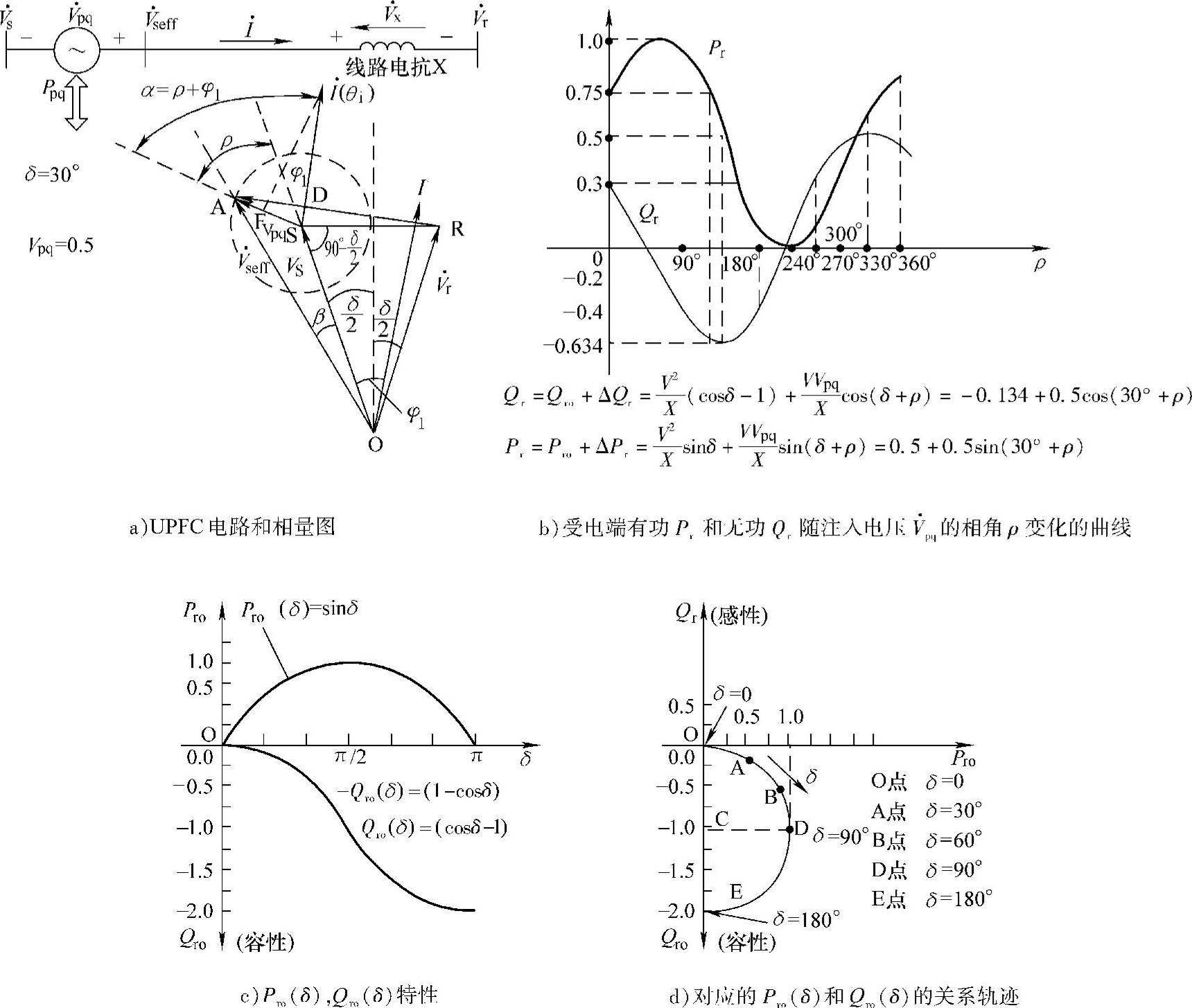
图7-6 UPFC电路相量图和功率特性

若V_r=V_s=V_R，取电压基准值为V_R，功率基准值为V²_R/X，若V_pq为补偿电压的相对值，P_pq、Q_pq也是相对值，则有(www.xing528.com)

P_pq=V_pq[sin（δ+ρ）-sin ρ] （7-9C）

Q_pq=V_pq[Vpq^+cos ρ-cos（δ+ρ）] （7-9D）

忽略线路电阻R，线路不消耗有功功率。补偿电压V_pq=0时，P_ro=P_so，有补偿电压V_pq后，变流器注入线路的有功功率P_pq加首端功率增量ΔP_s应等于末端功率增量ΔP_r，即ΔP r=ΔP_s+P_pq。而线路电抗消耗的无功功率I²X（标幺值）应是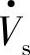输出的感性无功Q_s、末端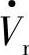向线路输出的感性无功-Q_r和串联补偿电压V_pq向线路注入的感性无功Q_pq之和，即I²X=Q_s+（-Q_r）+Q_pq。

由式（7-3A）、式（7-3B）中的ΔP_r、ΔQ_r及式（7-8C）、式（7-8D）中的ΔP_s、ΔQ_s，还可求得串联补偿电压的幅值V_pq和相角ρ与ΔP_r、ΔQ_r、ΔP_s、ΔQ_s的函数关系。

补偿电压幅值为

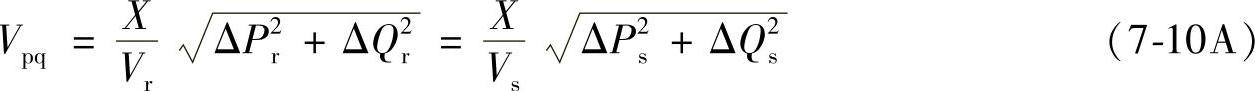
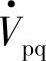超前V_s的相角为

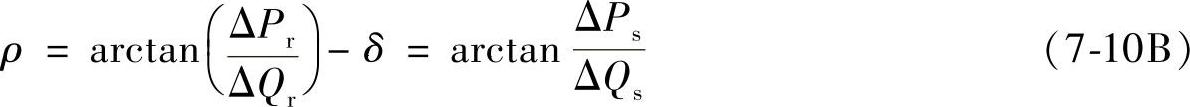
如果上两式中的ΔP_r、ΔQ_r、ΔP_s、ΔQ_s为指令值，则可由上两式得到与此对应的补偿电压的幅值V_pq和相位角ρ指令值。对任何一组指令值ΔP_r、ΔQ_r都可求得一组V_pq和ρ或相量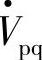，因此UPFC可实现P_r、Q_r的独立控制。

不同相位角ρ的补偿电压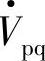具有多种不同的补偿控制功能。图7-7画出了线路注入补偿电压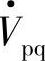后能实现的6种串联补偿功能的相量图。

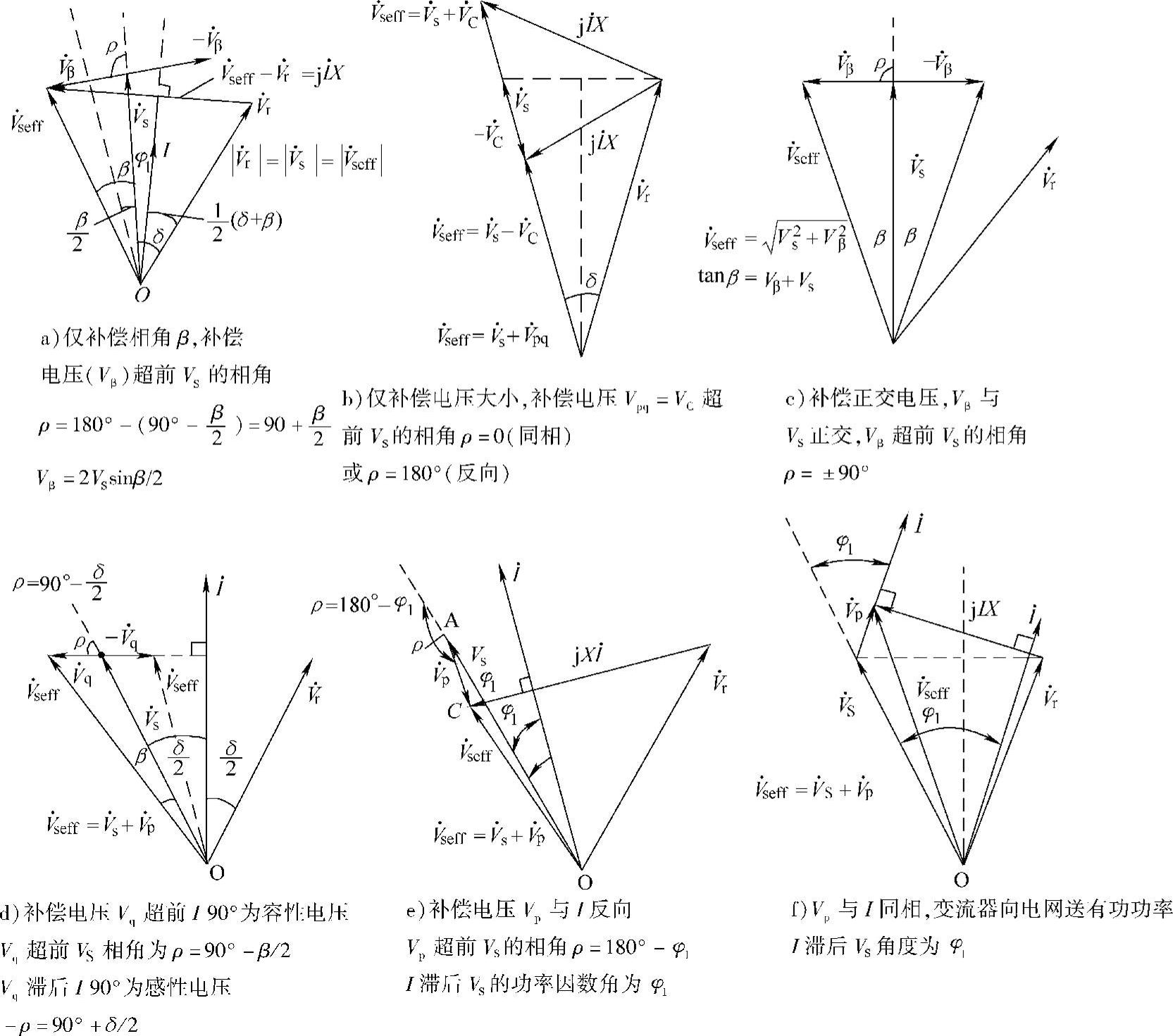
图7-7 用以说明UPFC对输电控制能力的相量图

1.补偿电压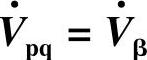仅用于移相（见图7-7a）

图7-6a中首端电压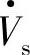补偿为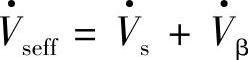后电压大小不变V_seff=V_s，但补偿后与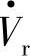之间的功角从δ变为δ+β。6.5.2节已分析这种移相补偿器，补偿电压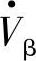相位超前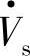的角度ρ=90°+β/2，V_β=2V_s sin β/2，β=2arcsin（V_β/2V_s）。补偿前后功率P_r、Q_r、ΔP_r、ΔQr等为式（6-19），移相补偿电压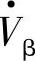注入线路的功率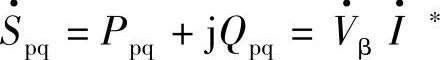。由于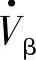与电流I·并不正交，因此移相补偿时变流器与电网线路之间既有有功功率又有无功功率交换，这时变流器直流侧应有直流电源。由图7-4的统一潮流控制器（UPFC）的并联变压器、变流器Ⅱ提供直流功率，使变流器Ⅰ输出串联移相电压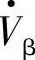，改变线路首端电压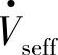的相位角，控制线路潮流。

2.补偿电压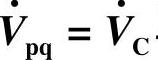与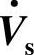同相或反相（见图7-7b）

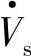仅补偿电压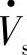的幅值并不改变补偿后线路首端电压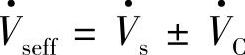的相位，这时补偿后的P_r、Q_r、ΔP_r、ΔQ_r为式（6-17）。这时同相或反相补偿电压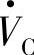与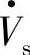一样向线路注入有功和无功补偿。

3.补偿电压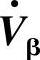与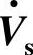正交（见图7-7c）

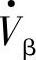超前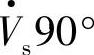（或滞后90°），补偿后线路首端电压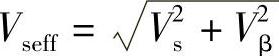，移相角β=arctanV_β/V_s。由于V_seff略大于V_s，因此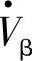使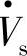移相β的同时，还使V_seff略有增大，这种正交移相升压器可以由变压器-晶闸管移相器（图6-41a）实现，但它并不是理想的纯移相器，移相后的P_r、Q_r、ΔP_r、ΔQ_r为式（6-22）。功角特性参见图6-41b。

4.补偿电压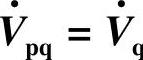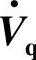，与电流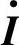正交（见图7-7d）

这种方式仅可实现容性或感性无功补偿。由于注入电压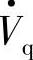与电流I·正交，故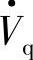注入线路的有功功率为零，V_q注入线路的无功功率为V_qI。补偿后P_r、Q_r、ΔP_r、ΔQ_r为式（6-13），功角特性为图6-24所示。

5.补偿有功电压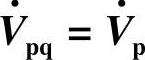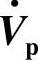，与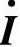反相（见图7-7e）

图7-7e中补偿电压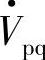仅为负值有功电压，串联变流器输出负值有功功率或串联变流器从电网线路吸收有功功率，这时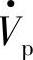超前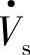的相角ρ=180°-φ₁（φ₁为电流I·滞后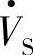的功率因数角），由式（7-1）、式（7-2）和式（7-9）可得到

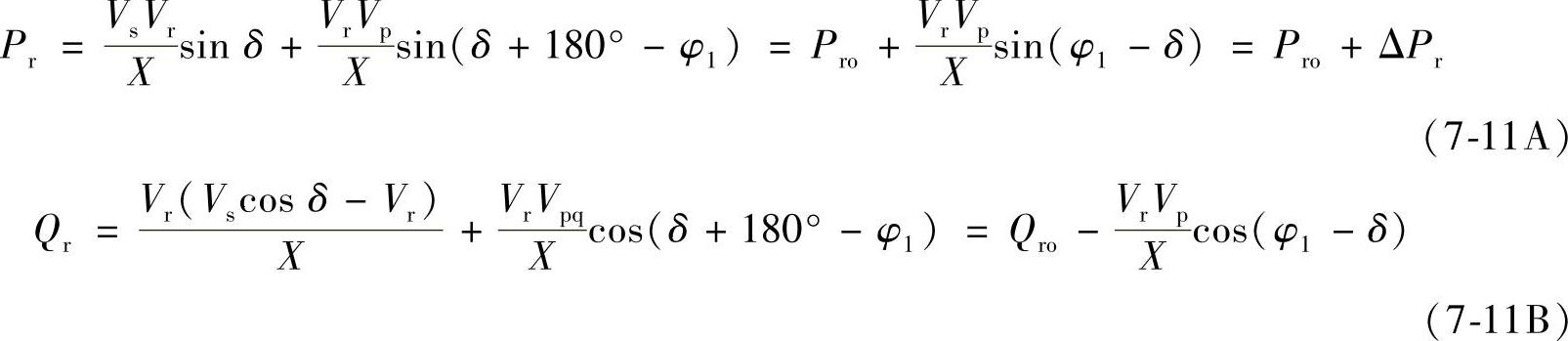
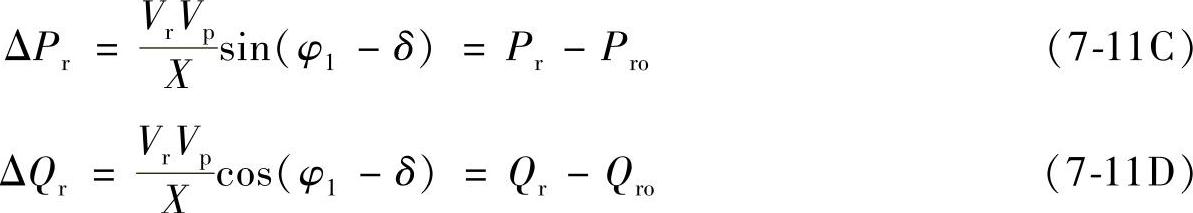
当补偿电压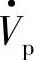与电流I·反相时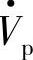，与电流I·所形成的向电网线路输出的有功功率Pp和感性无功功率Q_p为

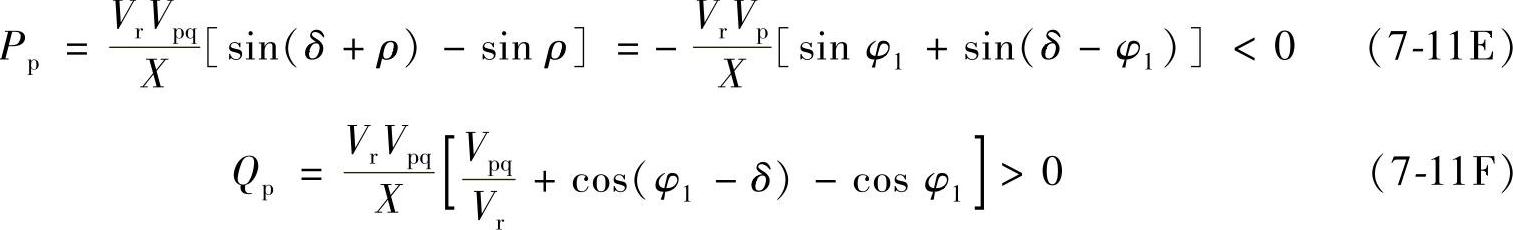
6.补偿有功电压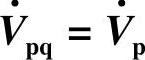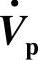，与线路电流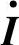同相（见图7-7f）

图7-7f画出了变流器输出正值（与电流I·同相的）有功补偿电压V_p时的相量图，可用于变流器向电网线路输出有功功率；补偿线路电阻电压降，提高线路等效阻抗比（X/R）。

由图7-4c可知UPFC输出的补偿电压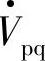可实现节点电压幅值调节、传输角调节及改变线路等效阻抗等各种补偿功能，而一般的串联或并联补偿器则只能完成单一功能。若将图7-4c中的补偿电压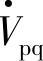分解为与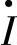正交的无功补偿电压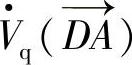和与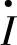同相的有功补偿电压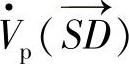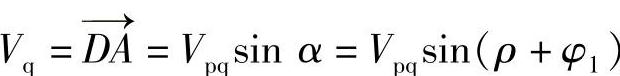，，V_p=SD=V_pqcos（ρ+φ₁），调控V_pq的大小和相位角ρ，可独立调控有功和无功串联补偿电压V_p、V_q，维持或改变线路有功或无功潮流，满足系统运行指令要求。