图6-31a中输电线路电阻为R,等效电抗为Xeff,线路阻抗角为φ,tgφ=Xeff/R,线路阻抗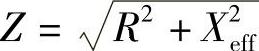 ,若线路末端电压
,若线路末端电压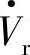 与首端电压
与首端电压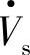 之间的相位差为δ,且在数值上Vr=Vs=V,由式(1-16C)、式(1-16D)、式(1-17C)、式(1-17D)可得线路首端有功功率为
之间的相位差为δ,且在数值上Vr=Vs=V,由式(1-16C)、式(1-16D)、式(1-17C)、式(1-17D)可得线路首端有功功率为
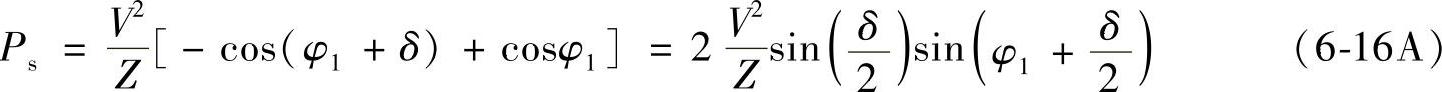
线路首端滞后无功功率为
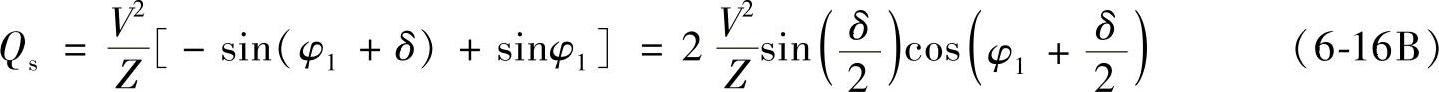
线路末端有功功率为
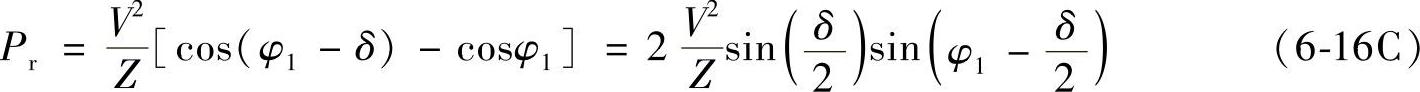
线路末端滞后无功功率为
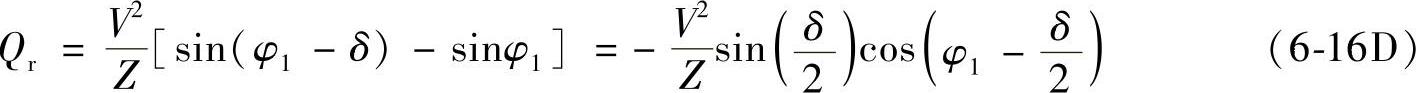
Qr为负值,表明线路末端电源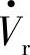 也必须向线路输出感性无功-Qr,这时Qs+(-Qr)共同向线路提供无功损耗I2X。
也必须向线路输出感性无功-Qr,这时Qs+(-Qr)共同向线路提供无功损耗I2X。
线路有功损耗Px=Ps-Pr=2V2 cosφ1(1-cosδ)/Z=I2R
线路无功损耗Qx=Qs-Qr=2V2 sinφ1(1-cosδ)/Z=I2X
末端无功对有功功率的比值为
Qr/Pr=1/tg(φ1-δ/2) (6-16E)
对于理想输电线路R=0,线路阻抗角φ1=arctanXeff/R=90°,且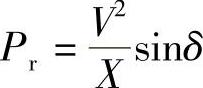 ,δ=δm=90°时,出现Prmax=V2/X,稳定运行区为δ=0→90°。
,δ=δm=90°时,出现Prmax=V2/X,稳定运行区为δ=0→90°。
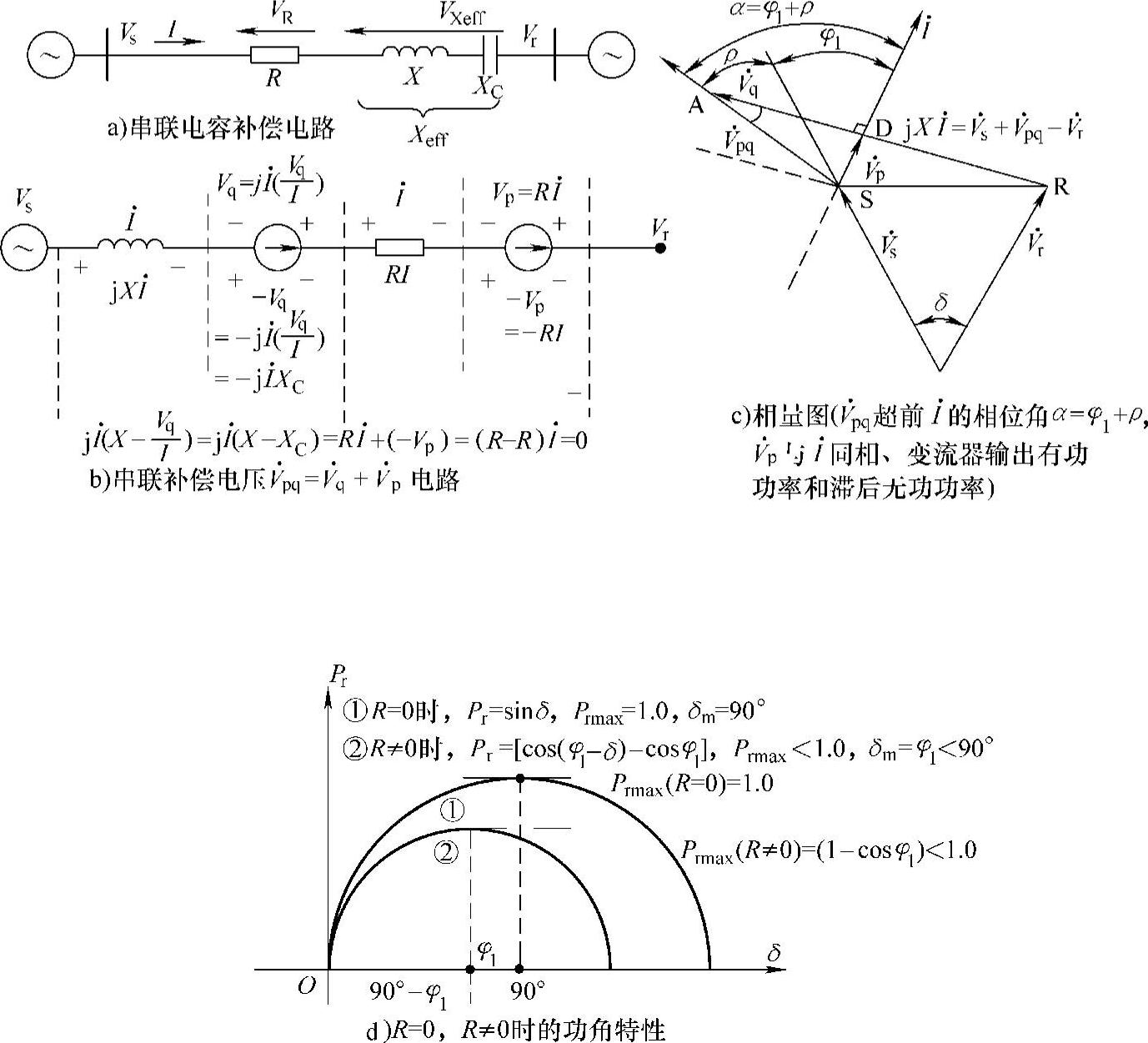
图6-31 线路阻抗比对串联电容补偿增加功率传输量的限制
对于实际线路R≠0时,φ1=arctan(Xeff/R)<90°,由式(6-16C),令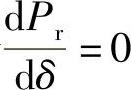 可求得出现最大Prmax时的功率角δm=φ1=arctan(Xeff/R),最大传输功率为
可求得出现最大Prmax时的功率角δm=φ1=arctan(Xeff/R),最大传输功率为

这时的最大无功功率为(https://www.xing528.com)

稳定工作区为δ=0→δm=φ1=arctan(Xeff/R),若线路电阻R大,Xeff减小,线路阻抗比Xeff/R减小,则φ1=arctan(Xeff/R)减小,输电系统传输特性全面变坏:稳定运行区从δ=0~90°缩小变为δ=0→φ1,最大传输功率Prmax减小,Qr绝对值变大,线路有功损耗增大,传输单位有功所需的无功值Qr/Pr增大。线路等效电阻R越小,比值Xeff/R越大,φ1越大,输电系统传输特性越好。图6-31d示出了R=0和R≠0时的功角特性。
在输电线路中串联电容器的功能是作为一个容性电抗,仅能减小线路等效感性电抗或向电网提供容性无功功率,而SSSC却不同,通过控制注入电压的幅值及其与输电线电流的相位角差的大小,就可以与电网系统交换无功或/和有功功率或通过在线路中注入补偿电压而调控线路等效的电抗或/和电阻。当然,交换有功需要在SSSC变流器的直流端有一个电源或适当的储能设备。
SSSC与电网交换有功的能力有很大的应用潜能。一个重要的应用是通过向线路串联注入有功补偿电压Vp和无功补偿电压Vq可以同时补偿输电线串联电阻和电抗,以保持输电线有等值较高的X/R比值,改善输电特性。在许多应用中,特别是115kV,230kV和340kV电压等级的输电线,X/R比值通常比较低(3~10),采用高的串联容性补偿度会进一步减小X/R比值。理想的输电线R=0,X/R=∞,线路阻抗角φ=arctan(X/R)=90°。若图6-31a中若无补偿输电线的X/R比值为7.4,线路阻抗角φ=82.3°,当增加串联容性补偿度为50%时,等效电抗电阻比Xeff/R=(X-XC)/R将减小为3.7,φ角则减小到74.9°串联电容补偿虽然减小了线路等效电抗但输电特性并不好。图6-31b、c示出了在线路中引入串联同步补偿器SSSC补偿电压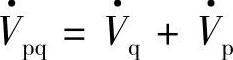 的等效电路和相量图。图中,φ1是
的等效电路和相量图。图中,φ1是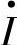 滞后
滞后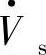 的相位角,
的相位角,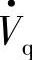 与电流
与电流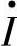 正交,与线路电抗电压降
正交,与线路电抗电压降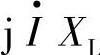 同相,类似于串联电容补偿线路电压降;补偿电压
同相,类似于串联电容补偿线路电压降;补偿电压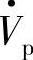 则与电路I·同相,与线路中电阻电压降I·R同相,可补偿线路电阻电压降。
则与电路I·同相,与线路中电阻电压降I·R同相,可补偿线路电阻电压降。
在标幺制中取V2/X=1,由式(6-16C)、式(6-16D)两式可得到用标幺值表示的首端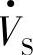 传输至末端的有功功率Pr、末端电源
传输至末端的有功功率Pr、末端电源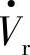 提供给线路的滞后无功无功功率Qr与传输角δ的特性。以比值Xeff/R为参数变量的函数关系曲线如图6-32所示(Xeff/R分别为∞、7.4、3.7,阻抗角arctanφ=Xeff/R,阻抗
提供给线路的滞后无功无功功率Qr与传输角δ的特性。以比值Xeff/R为参数变量的函数关系曲线如图6-32所示(Xeff/R分别为∞、7.4、3.7,阻抗角arctanφ=Xeff/R,阻抗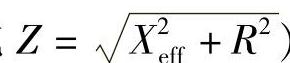 。
。
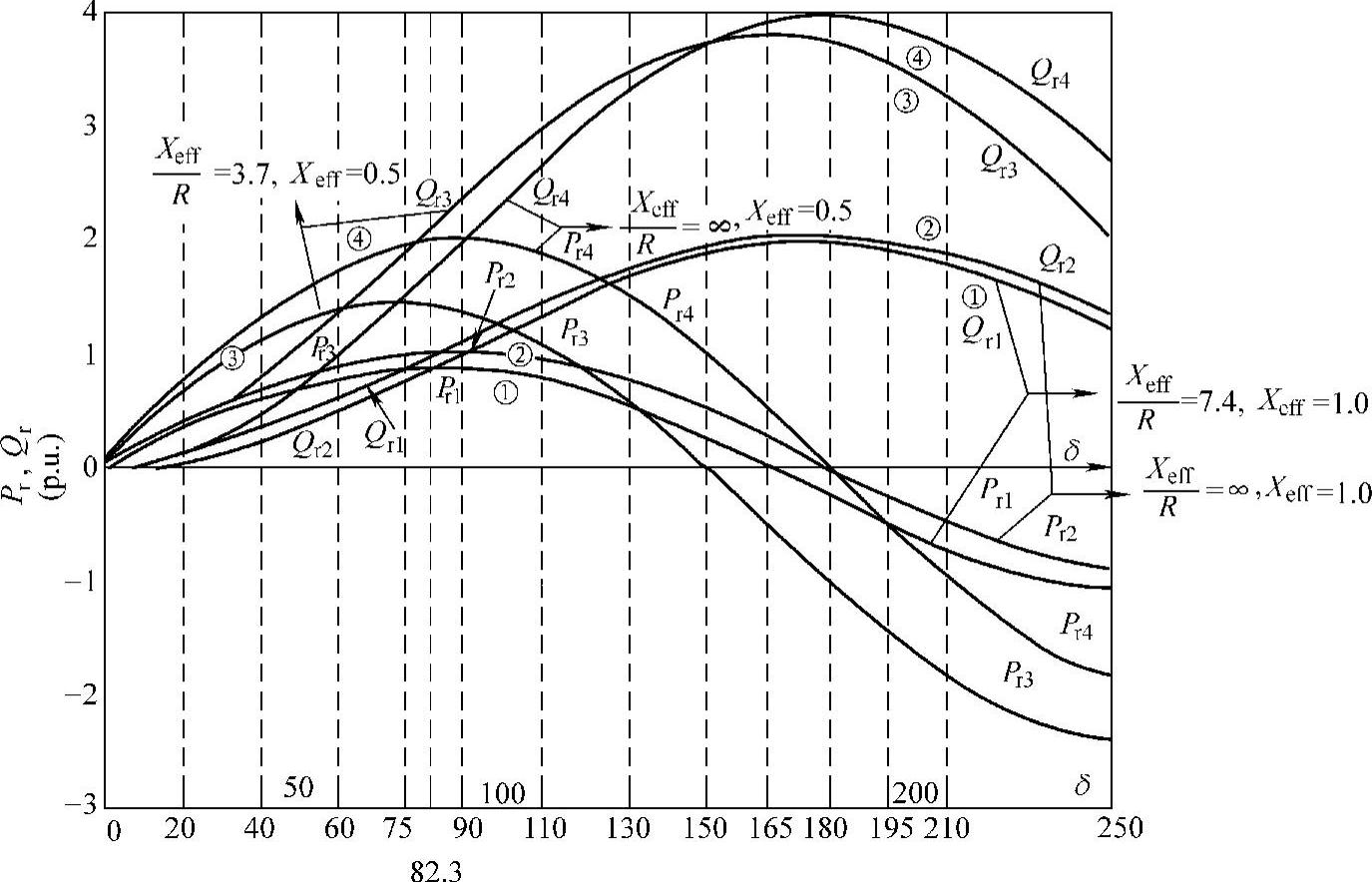
图6-32 以线路阻抗比Xeff/R为参变量的有功功率Pr和无功功率Qr与传输功率角δ的关系
作为一个算例,利用式(6-16)各式可计算四种工况下输电系统的运行特性Pr、Qr:
1)实际线路无任何补偿,线路等效电抗Xeff=X,令Xeff/R=X/R=7.4,阻抗角φ=83.2°时的Pr1、Qr1,如图6-32中曲线①所示。
2)将实际线路看作R=0的理想线路或引入SSSC通过补偿电压Vp引入有功阻性补偿,将实际线路的电阻R(电压降)补偿为零,实际线路电抗X不补偿,即Xeff=X,使Xeff/R=∞,φ=90°时的Pr2、Qr2,如图6-32中的曲线②所示。
3)实际线路有无功功率补偿度k=XC/X=0.5,Xeff=X-XC=(1-k)X=0.5X,线路无有功补偿,R不变,Xeff/R=3.7,φ=74.9°时的Pr3、Qre,如图6-32中的曲线③所示。
4)线路有无功功率补偿,补偿度k=0.5,Xeff=0.5X,同时又有有功补偿使等效R=0,Xeff/R=∞,φ=90°时的Pr4、Qr4,如图6-32中的曲线④所示。
表6-1 四种工况功率特性计算结果
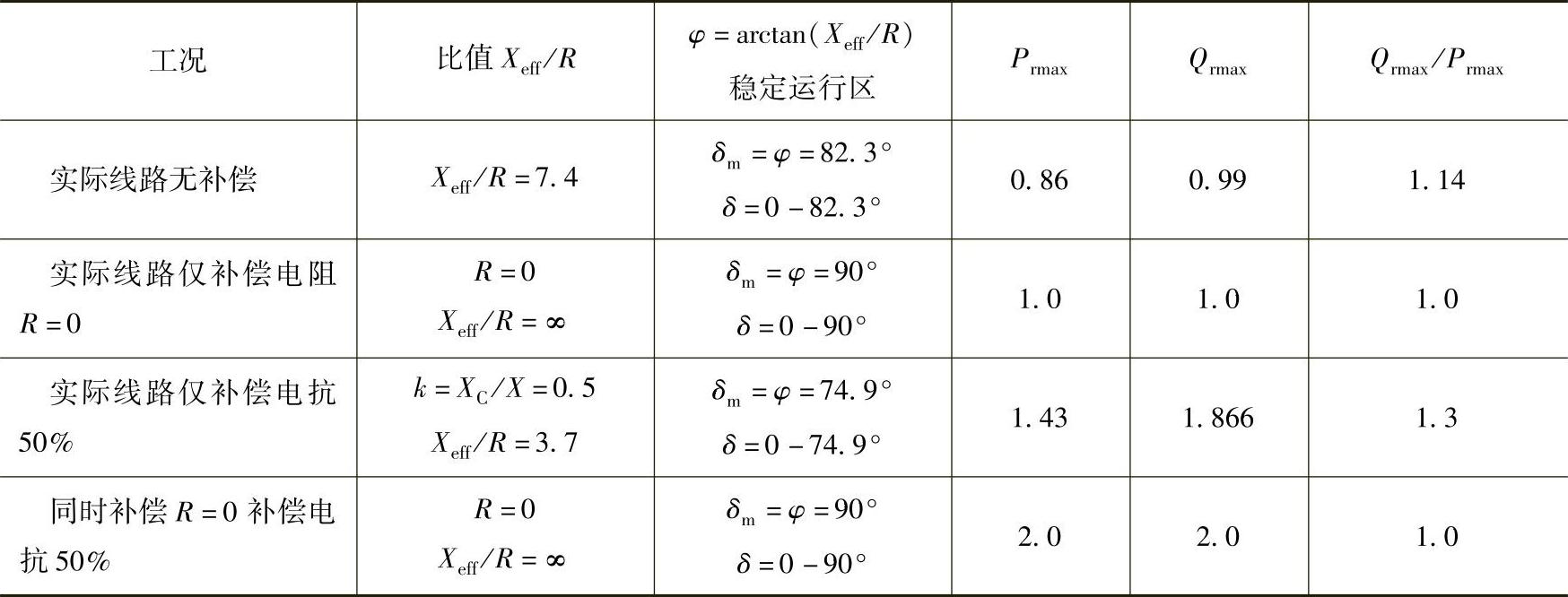
表6-1给出了图6-32中画出的四种工况下的功率特性Pr=f(δ,φ1)、Qr=f(δ,φ1)和Qrmax/P rmax的计算结果。数字结果是:第一种情况未经补偿的实际输电线X/R=7.4,φ=82.3°,由于R≠0,φ1≠90°使传输功率Pr1与理想输电线Pr2(第二种情况Xeff=X,R=0,仅采用电阻补偿使φ1=90°)相比较,Pr1的最大可能传输功率Pr1max比Pr2max下降约14%,比值Qrmax/P rmax增大约14%,Pr1max出现在δ=90°-φ1=82.3°处,稳定工作区(dPr/dt>0)为δ=0~82.3°。第三种情况仅有串联电抗补偿,补偿度k=0.5,使Xeff=0.5X,Xeff/R=3.7,φ1减小到φ1=74.9°,R仍为实际线路电阻,这时最大传输功率Pr3max出现在δm=φ1=74.9°处,第三种工况Xeff/R=3.7,Pr3max较第一种工况(Xeff/R=7.4)的Pr1max要大66%,而比值Qrmax/Prmax则上升约15%,稳定工作区为δ=0~74.9°。因此串联电容补偿,即使将线路电抗减少一倍,Xeff=0.5X,Prmax也不能增大一倍,且稳定运行区从0~82.3°变小为0~74.9°。第四种工况同时补偿电阻和线路电抗,使等效电阻R=0,线路电抗减半,则稳定运行区为δ=0~90°,同时Prmax增大一倍,且比值Qrmax/Prmax=1与理想输电线路相同。
因此,补偿线路电抗X可增大传输功率Pr的最大值,但使稳定运行区缩小,且末端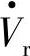 也必须向线路供给较大的滞后无功。同时补偿线路电阻和电抗才能构成一个理想的输电系统,获得优良的输电特性。
也必须向线路供给较大的滞后无功。同时补偿线路电阻和电抗才能构成一个理想的输电系统,获得优良的输电特性。
输电线路采用静止同步串联补偿器(SSSC)提供有功补偿可有效用于几条X/R比值不同的并行输电线,通过平衡有功和无功潮流使循环功率最小。
为了能给输电线路提供有功补偿,串联注入电压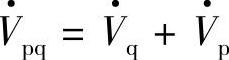 中,必须有与线路电流同相的有功补偿电压
中,必须有与线路电流同相的有功补偿电压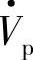 ,
,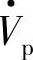 与电阻电压降I·R大小相等、方向相反。Vp补偿电阻电压降使线路等效电阻为零,这时开关型变流器的直流侧必须有直流电源,使变流器通过在线路上注入有功补偿电压
与电阻电压降I·R大小相等、方向相反。Vp补偿电阻电压降使线路等效电阻为零,这时开关型变流器的直流侧必须有直流电源,使变流器通过在线路上注入有功补偿电压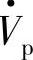 补偿线路R的有功损耗.当然也可通过注入
补偿线路R的有功损耗.当然也可通过注入 与线路交换有功功率。
与线路交换有功功率。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




