传输功率与传输角的关系函数研究

图6-23a中补偿电压V_q是超前线路电流I·90°的感性无功补偿电压，等效于线路中引入了一个补偿电容。若V_r=V_s=V，有串联补偿电压V_q后，线路首端电压增大为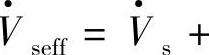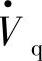，与末端电压之间的相位差变为β+δ，输电线传输功率从无功补偿电压V_q时的P_ro、Qro增加ΔP_rq、ΔQrq，有补偿电压V_q后，类似式（6-1）、式（6-3），线路传输至末端的功率为P_rq=P_ro+ΔP_rq，Q_rq=Q_ro^+ΔQ_rq。

由图6-23a中的相量图，有

由式（6-11）得到

取电压基准值为额定电压V_R，则电压标幺值为V∗=V_q/V_R，V_q∗=V_q/V_R；取功率基准值为V²_R/X（X为线路电抗），则功率标幺值为P_rq∗=P_rqX/V²_R；Q_rq∗=Q_rqX/V²_R，电抗标幺值为X∗=X/X=1.0。如果输电系统中电压V_s=V_r=V=V_R，则式（6-12A）、式（6-12B）的标幺值功率为

P_rq∗=sinδ+V_q∗cos（δ/2） （6-13A）

Q_rq∗=（cosδ-1）-V_q∗sin（δ/2） （6-13B）

又无补偿时（V_q=0）的功率P_ro∗、Q_ro∗为

P_ro∗=sinδ （6-13C）

Q_ro∗=cosδ^-1 （6-13D）

补偿电压V_q引起的传输功率增量ΔP_r∗、ΔQ_r∗为

ΔP_rq∗=V_q∗cos（δ/2） （6-13E）

ΔQ_rq∗=-V_q∗sin（δ/2） （6-13F）

请注意：为书写简便，以下各功率表达式中的电压功率标幺值的下标符号∗一般不再加注。

给定串联补偿电压V_q后，由式（6-13A）可画出传输有功功率P_rq与相角δ的函数特性，由式（6-13A）可求得在一定的V_q值时P_rq的最大值P_rqmax及其对应的δ_m值。由式（6-13A），并令dP_rq/dδ=0，可求得

由上式得到：(www.xing528.com)

由式（6-13A），在δ=δ_m时的P_rqmax为

按式（6-13A），图6-24画出了V_q=0（无补偿），V_q=±0.345，V_q=±0.67时的P_rq=f（V_q，δ）特性，无补偿时（V_q=0）最大传输功率出现在δ_m=90°，随着正值V_q的增大，δ_m从90°减小，δ=δ_m时的最大功率P_rqmax增大；随着负值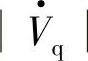的增大，δ_m从90°增大，P_rqmax减小。

当V_q=0.345、0.67时，由式（6-14B）、式（6-14C）可得到：δ_m=83.4、77.84；P_rqmax为1.25、1.5。

下面分析图6-1中有串联电容容抗X_C补偿时输电线的传输功率P_rC。如果无补偿时线路电抗为X，V_s=V_r=V，由式（6-5A）可得到在相对单位制中，有

δ=90°有最大功率，标幺值为

当k=0.2时P_rCmax∗=1.25；k=1/3时P_rCmax=1.5。

如果串联补偿电压V_q与串联电容补偿电抗X_C有相同的最大功率，则有

串联电容不同补偿度时，功率P_rC与传输角δ的关系如图6-25所示。对比图6-24和图6-25可知，要达到相同的最大功率值、串联电容补偿时的k=0相当于串联电压补偿时的V_q=0，这时P_max=1.0；串联电容补偿时k=1/5、1/3，相当于串联电压补偿时的V_q=0.345、0.67，最大功率分别为1.25、1.5。

串联电容补偿时无论补偿度k=X_C/X为何值，最大传输功率P_rCmax都出现在δ_m=90°，但串联补偿电压V_q不同时，输出最大传输功率P_rqmax时的功率角δ_m随V_q的不同而不同。当V_q=0时δ_m=90°，V_q为正值时δ_m从90°减小，V_q为负值时δ_m从90°增大，当δ<δ_m时δ增大时P_rq增大，当δ=δ_m时P_rq达到P_rqmax，δ超过δ_m后，δ再增大，P_rq反而减小。

图6-24 以电压源变流器串联补偿电压V_q为参变量的传输功率和输电功率角δ函数关系

图6-25以串联电容的补偿度k为参变量的传输功率和输电功率角的功角的函数关系

通过比较图6-24与图6-25所示的曲线，可以看出串联电容器补偿输电线的传输功率增加的百分率（与无补偿的输电线相比，P_rC/P_ro=1/（1-k））仅与补偿度k有关而与δ无关，而有静止同步串联补偿器（SSSC）的输电线最大传输功率增加的百分率P_rq/P_ro=1+V_q∗/（2sinδ/2），不仅与补偿电压V_q∗有关而且与δ有关。

在第5章中电压源型静止同步并联无功补偿器STATCOM输出的无功电流可为容性，也可为感性。与STATCOM类似，电压源型静止串联补偿器输出的电压可为容性，也可为感性（V_q可正、可负）。为了稳态和动态潮流控制的应用需要，静止同步串联补偿器（SSSC）与STATCOM一样，也可有2倍变流器额定容量宽度（如从V_q=-0.7到V_q=+0.7）的控制补偿范围。这意味着SSSC既可以减少又能增加相同的（传输）功率。只要简单地改变注入补偿电压的极性就可以满足要求。由图6-23可知，当V_q为图中所示正方向时，使电流I增大，图6-24或式（6-13A）中的P_rq也增大。若V_q为负值，即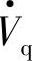反向时，则电流I减小，P_rq减小。当V_q负值很大时，传输功率P_q可能变为负值，如图6-24中所示，就实现了传输功率的“潮流反转”。

除了有容性、感性双向补偿能力外，SSSC的基本运行特性与串联电容器补偿主要的不同点是SSSC实际输出的是串联补偿电压而不是容抗，当然不会与线路电感形成串联谐振，因为SSSC插入线路的串联补偿电压由控制系统设置且可独立于输电线电流。