串联电容补偿的基本功能介绍

串联电容补偿是电力系统中使用最早、应用最多、经济性和运行效能都较好的串联补偿装置。其工作原理虽然比较简单，但可为其他较复杂的串联补偿装置的分析、研究提供一些基本概念。

串联电容补偿的基本思想是减小输电线路从送端到受端的等效电抗，图6-1a是一个两端电源系统模型，相应的电压和电流相量图如图6-1b、c所示。

图6-1 串联补偿原理图

若线路电抗为X，且首、末端电压相等，V_s=V_r=V，无串联电容补偿时，由式（1-10）、式（1-11）、式（1-9B）可得，首端电源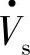输出的有功功率P_so、感性无功功率Q_so，以及首端电源V·_S经输电线路电抗X传送至线路末端电源处的有功功率P_ro和感性无功功率Q_ro为

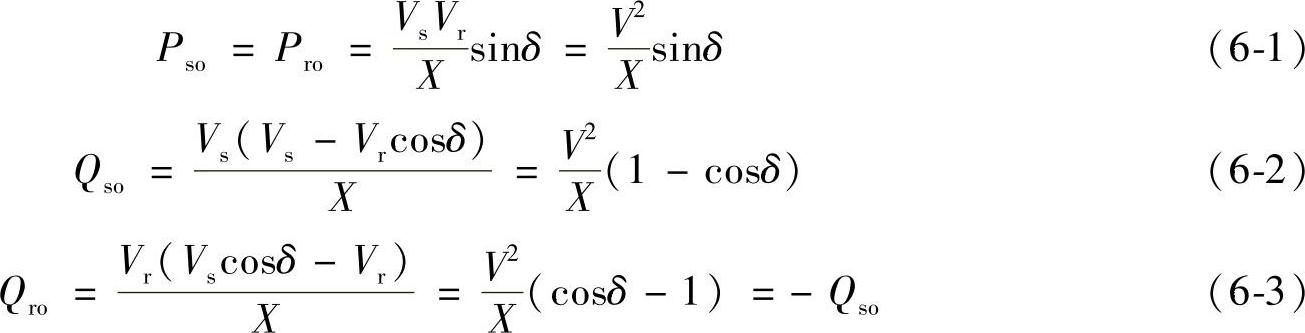
由式（6-2）和式（6-3）可知，在V_s=V_r时，首端电源V_s向线路输出感性无功功率Q_so，且Qso为正值，而这时经线路输入至末端电源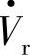处的感性无功Q_ro=-Q_so为负值，这表明V_r=V_S时为了经线路电抗X传输有功功率P_so=P_ro至末端，末端电源在接收有功功率的同时也必须向线路输出感性无功功率-Q_ro=Q_so，即首、末两端电源共同分担线路传输有功功率时线路电抗X的无功损耗为Q_x=I²X=Q_so+（-Q_ro）=2Q_so。

有串联电容C补偿后输电线路等效电抗为

X_eff=X-X_C=（1-k）X （6-4A）

式中，串联补偿电容C的容抗X_C=1/2πfC；k为串联补偿度，定义为

k=X_C/X，且0≤k≤1 （6-4B）

有串联电容补偿后线路传输至末端的有功和感性无功功率为P_ro=P_ro+ΔP_ro，Q_rC=Q_ro+ΔQ_rC，其中ΔP_rC、ΔQ_rC是串联补偿电容后增加的传输功率。

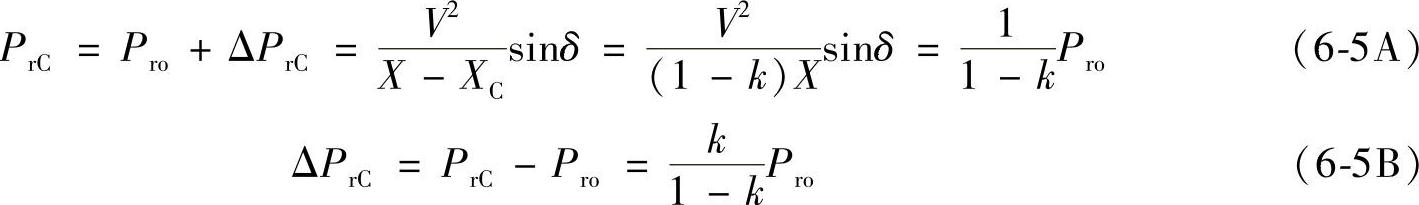
类似式（6-2），串联电容补偿后线路首端V_s输出的感性（滞后）无功为

由图6-1c可知，，I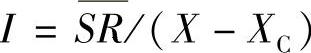，，因此串联电容提供的无功补偿功率为

由式（6-5C）、式（6-5E）可知，在V_s=V_r工况下，与无补偿时的情况一样，有补偿后，线路两端电源也都向线路传送相等的滞后无功，供线路电抗X无功损耗。

线路电抗X消耗的无功Q_X为(www.xing528.com)

在不同的补偿度下，线路传输的有功功率P_rC，串联电容补偿的无功功率Q_C和功率角δ的关系如图6-1d所示。补偿度k增加，传输功率P_rC迅速增加。同时，串联电容器提供的无功补偿功率Q_C也随着k的增大而增大，并且与线路无功功率损耗一样随着功率角δ而变化。图6-1d中P_max是无串联补偿（k=0）时，δ=90°线路传输功率的极限值，P_max=V²/X，有串联电容补偿后k≠0，δ=90°时最大传输功率P_maxC增大1/（1-k）倍。

串联补偿的基本功能如下：

（1）串联接入电容补偿部分线路感抗，提高输电线路的传输功率极限值

在图6-1d和式（6-5A）中，补偿度k=X_C/X=0.4时，δ=90°时的极限输电功率：P_rCmax/P ro=1/（1-k）=1.67，即补偿度k=0.4时将使静态极限传输功率提高67%。

（2）使电压稳定

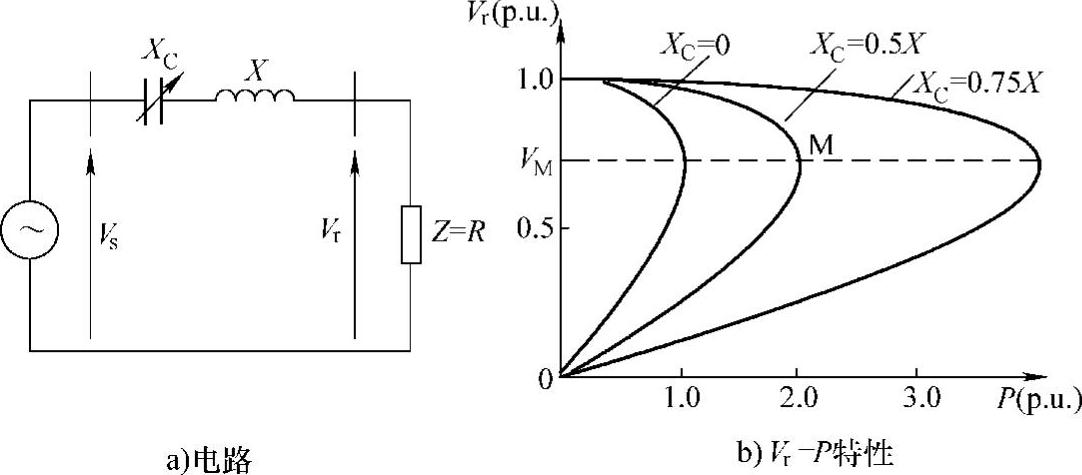
图6-2 传输线可传输功率和电压稳定极限与串联电容补偿的函数关系

串联电容也能够通过降低等效的线路电抗来减小受端电压波动和电压崩溃的可能性。一个简单的辐射型输电系统如图6-2a所示，其中X为线路电抗，X_C为串联补偿电抗，负荷阻抗为Z。图6-2b是在同一负荷功率因数下对应不同串联电容补偿度的V_r-P曲线。对应给定补偿水平的每条曲线的“鼻点”M（最大功率点）代表了相应的电压不稳定点。M点电压V_M为临界电压，V<V_M不能稳定工作，容抗补偿X_C越大，稳定工作区所对应的P_M也越大。并联补偿感性无功负载和串联电容补偿都能够有效地增加电压稳定性，但并联补偿通过提供无功功率和调节终端电压改善电压稳定性，而串联电容补偿则通过抵消线路部分电抗从而向负荷提供一个“刚性”电压源来实现电压稳定。为了提高输电的电压稳定性能，串联电压补偿比相同补偿容量的并联电流补偿效率更高。

（3）改善暂态稳定性

以6-1a所示简单系统为例。为简化分析，假设故障前和故障排除后系统结构保持不变，有串联电容补偿和没有串联电容补偿线路传输功率均为P_e0（发电机电磁功率），有补偿系统和没有补偿系统在相同时间承受同样的故障。这时系统的动态行为可用图6-3进行分析。故障前稳态运行时原动机输入的功率为P_e0，图6-3所示两种情况下故障前传输功率P_e0分别对应功角δ₁和δ_s1，P_e0=P₀（δ_s1<δ₁）。在短路故障期间，传输功率为零，而原动机输入功率P₀仍保持不变，所以送端发电机功角从稳态时的δ₁和δ_s1分别增加到故障清除时的δ₂和δ_s2，加速能量可用图6-3中面积A₁和A_s1表示。故障切除后，电磁功率P_e大于原动机输入功率P₀，所以送端发电机从δ₂和δ_s2开始减速，减速期间的减速能量用面积A₂和A_s2表示。当A₂=A₁和A_s2=A_s1，即达到加速能量和减速能量平衡时，电机相对速度为零，达到的最大功角分别为δ₃和δ_s3。无串联补偿时的暂态稳定裕度A_margin可以用P-δ曲线和P_e0直线（δ₃，δ_crit）围成的面积表示，同理有串联补偿时的暂态稳定裕度也可以类似的用面积A_smargin表示。比较图6-3a和图6-3b可以看出，A_smargin>A_margm，即串联电容补偿大大增加了暂态稳定裕度。增加的暂态稳定裕度与串联补偿度成比例。从理论上说，可以设计X_C很大而使暂态稳定裕度增加到很大。但是，通常实用的串联电容补偿度k都不会超过50%，这是由于：k过大时平行线路的负荷平衡控制较困难，潮流控制也较困难；会使故障电流增大；容易引发次同步振荡问题，实际工程应用中串联补偿度常常限制在30%以下。

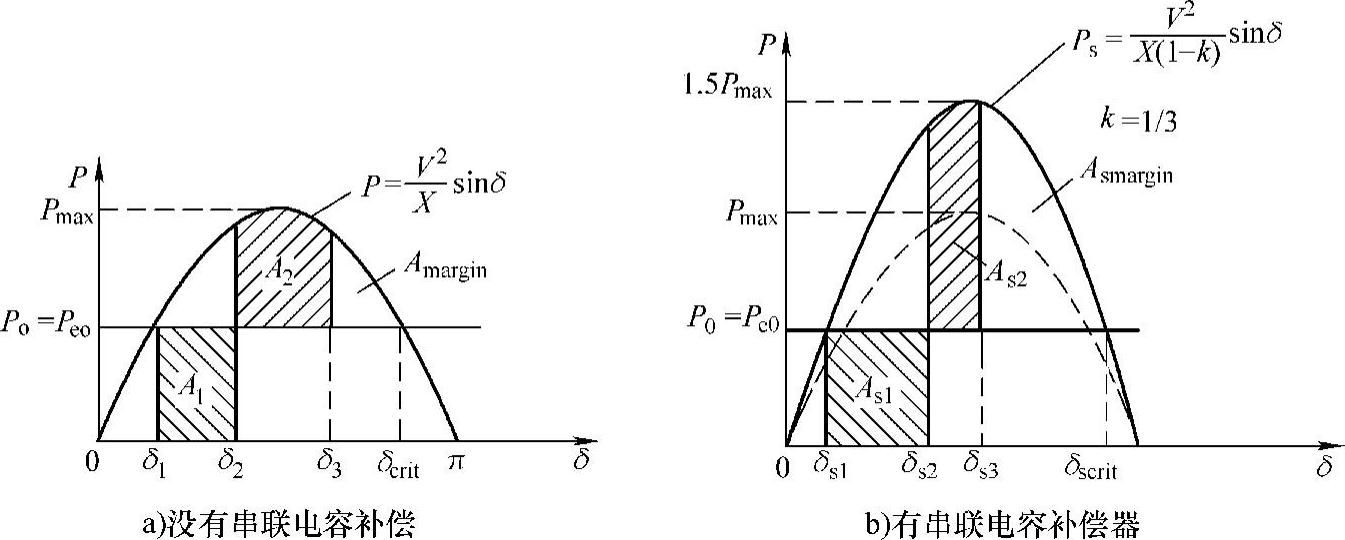
图6-3 用以说明简单双发电机电力系统的暂态稳定极限的等面积准则

（4）功率振荡阻尼

可控串联补偿通过改变串联补偿度k值能够用来有效阻尼系统功率振荡。正如第5章所解释的，要阻尼功率的振荡，应实时、适度改变投入的补偿量来抑制受扰机组的加速和减速摇摆。

图6-4a所示为有串联补偿有阻尼和无串联补偿无阻尼时功角δ对时间t的振荡曲线，图6-4b是发电机输出的有功功率P在有阻尼和无阻尼时的振荡曲线，图6-4c是为阻尼功率振荡串联补偿度k随时间变化的关系。图中，当发电机加速，功角δ增大，dδ/dt>0时，k应取最大值使P增大，阻尼转子加速；当dδ/dt<0，发电机减速，δ减小时，应取k为零，使P减小，阻尼转子减速。当k为最大时，线路阻抗最小，所以线路传输的电磁功率最大。当k为零时，线路阻抗最大，传输功率最小。为简化控制和加大阻尼力度补偿度k可以采用“砰、砰”控制方式。事实上，这种控制方式阻尼大幅度振荡最为有效。但是，要阻尼相对小的功率振荡，特别是在补偿度k值较高时，采用连续调节k的方式也许更好。

串联补偿主要用来提高输电功率和解决潮流控制问题，这些问题与线路等效长度和输电网络的结构有关系。通过线路的固定补偿能够缩短线路的电气长度满足增大功率传输的要求。而对应导致潮流不平衡以及环状潮流的电网结构问题，则要求串联补偿度可控。在柔性交流输电系统中，各种可控串联补偿将在如下几个方面具有至关重要的作用：维持指定线路的潮流，紧急情况下改变潮流路径，确保输电线路的最佳使用；提高输电线路的传输功率极限值；稳定电压、改善电压波动和阻止电压崩溃；改善系统稳定性并阻尼功率振荡等。

图6-4 采用可控制的串联补偿使功率振荡衰减的波形