并联型无源LC滤波器的基本特性

无源LC滤波器按其在主电路中的连接方式的不同可以分为并联、串联和混联三种，其中并联型LC滤波器是应用最为广泛的一种。根据结构的不同，无源LC滤波器又可以分为单调谐滤波器、双调谐滤波器、多调谐滤波器及高通滤波器等几种，在实际应用中常常将单调谐滤波器、双调谐滤波器、多调谐滤波器及高通滤波器组合使用。

1.单调谐滤波器

图5-36a中的L、C、R（R为电感的电阻，R很小）串联电路就是一个LC单调谐滤波器。图中负荷电流除基波电流i_L1外还有n次谐波电流i_Ln，电源经线路电感L_s、电阻R_s对负荷供电。

图5-36b为n次谐波的等效电路，对于n次谐波，L、C、R支路的阻抗为

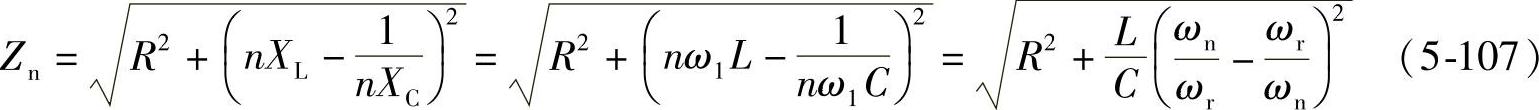
式中，ω_n=nω₁为n次谐波角频率，n=ω_n/ω₁为谐波阶次；ω_r为LC谐振角频率，ω_r=。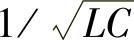

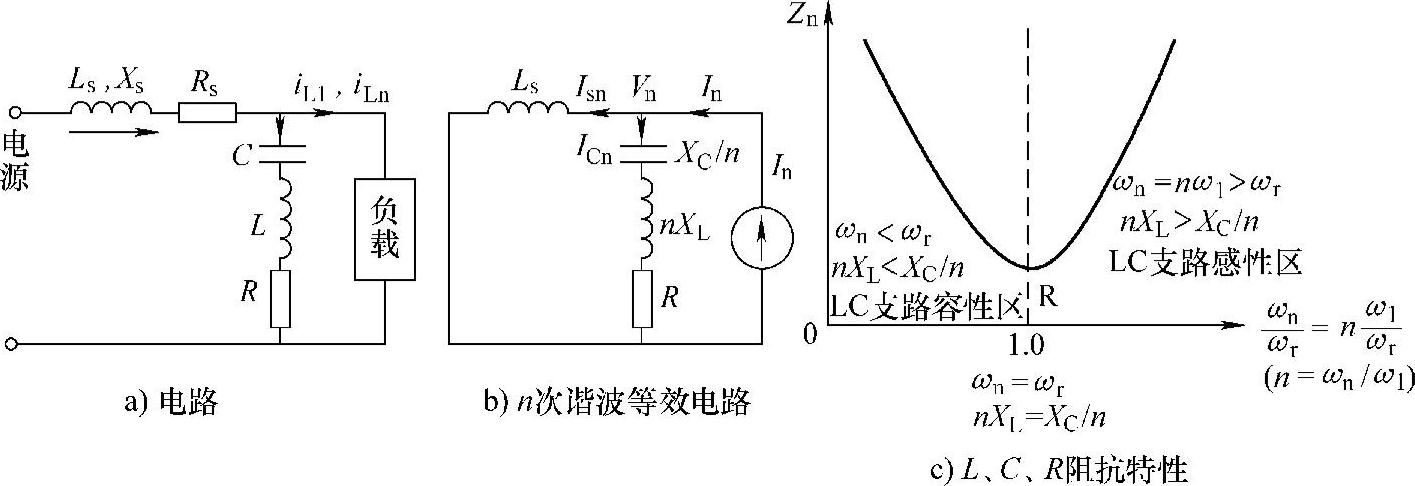
图5-36 单调谐LC滤波器特性

图5-36c为n次谐波阻抗Z_n与谐波频率相对值ω_n/ω_r的函数关系。当谐波频率ω_n=nω1等于LC谐振频率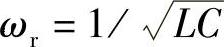时，即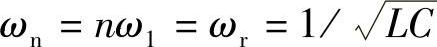，nX_L=nω₁L=1/nω₁C=X_C/n，或ω_n/ω_r=nω₁/ω_r=1时，则LC支路对n次谐波电流阻抗Z_n=R≈0，节点谐波电压V_n=RIn≈0，LC支路电流I_Cn≈I_n，流经电源支路的n次谐波电流I_sn≈0。而当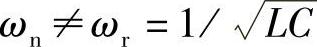（谐振频率）时，L、C、R支路阻抗Z_n=R≠0，电源支路的n次谐波电流I_sn≠0，节点谐波电压V_n≠0，LC滤波器起不到对n次谐波的全部滤波作用。由于LC支路只能对频率ω_n=ω_r=1/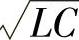的单一谐波滤波，故这种LC电路被称为单调谐滤波器。

为了使电源L_s支路中消除第n次谐波电流，只要选择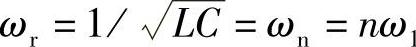，即LC的乘积LC=（1/nω₁）2即可。L选大些，C可选小些，或者L选小些，C应选大些都可以。但工程实际中为了能实现基波无功功率的补偿功能，除选用单独的并联型无功功率补偿支路外，也常常利用LC滤波器在基波电压作用下的等效无功补偿功能。例如，当LC滤波器的谐振频率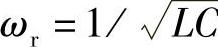按5次谐波f_n=5×50Hz、ω_n=2π×250Hz选择时，LC滤波器能使负荷电流中的5次（250Hz）谐波电流陷波，5次谐波的感抗等于5次谐波的容抗，“滤除”电源中的5次谐波电流，而这个L、C电路在节点基波电压的作用下，基波感抗小了5倍，基波容抗大了5倍。因此LC滤波电路对基波近似为一个容抗，对基波电压LC支路相当于一个并联电容器C，等效电容C的大小不同其基波的无功补偿作用也不相同。因此实际工程中选用LC滤波器的L、C参数时，不仅只考虑乘积LC=（1/nω₁）2，还必须考虑其基波无功补偿的要求。此外，在设计L、C数值大小时还必须考虑其他一些因数，其中最重要的是要防止电力系统中无源滤波器的电感L、电容C可能与电网线路电感L_s以及系统中并联的无功补偿电容形成串联或并联谐振，致使对某些频率的负荷谐波电流不仅起不到良好的滤波作用、抑制谐波电流，甚至还可能放大谐波电流。为了简便地分析L、C参数与线路电感L_s可能形成的谐振而使负荷谐波电流被放大的现象，从而得到较为清晰的近似的数量关系，假定图5_-36a中电源线路中R_s=0，LC支路中的R=0，负载n次谐波电流为I_n，分析图5-37b中谐波电流特性。

L、C支路的n次谐波电抗X_LCn，可由式（5-107）得到

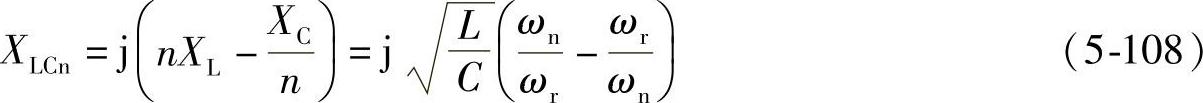
图5-37b中负荷谐波电流I·_n的一部分I·_Cn由L、C支路分流，其余部分I·_sn经L_s流入电源，L、C支路分流的n次谐波电流为

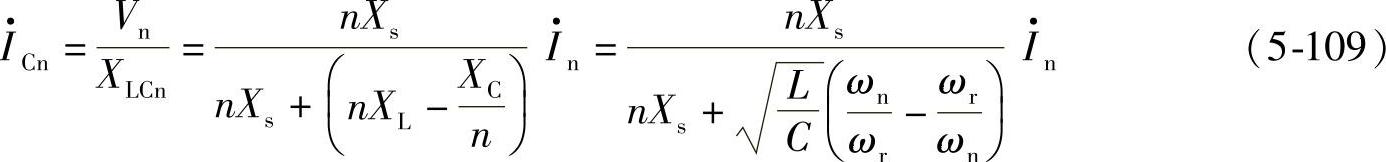
经L_s流入电源L_s支路的n次谐波电流I_sn为

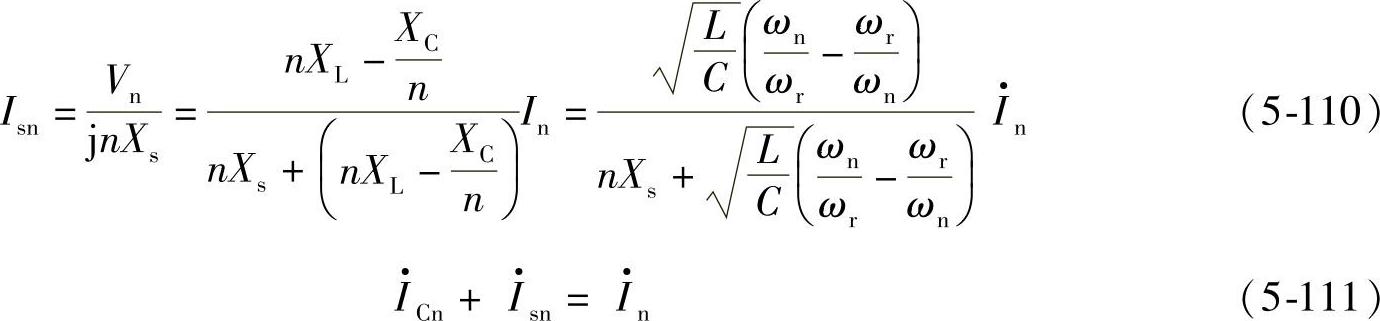
L、C滤波支路对负荷n次谐波电流的分流（分配）系数为

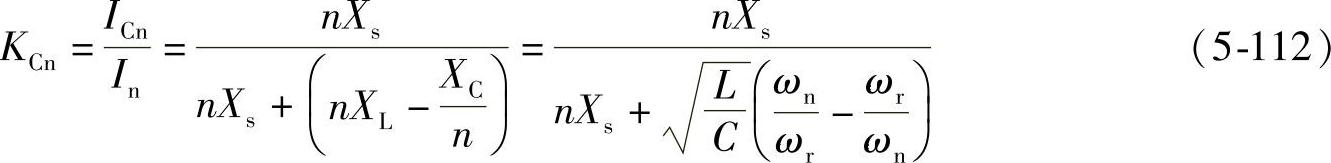
电源L_s支路对负载n次谐波电流的分流（分配）系数为

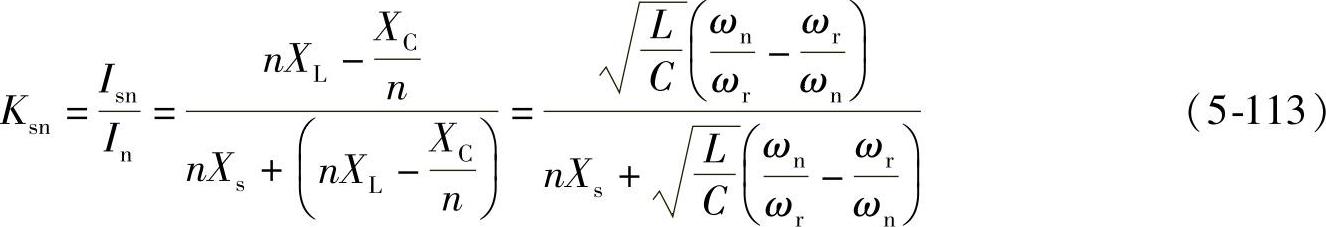
图5-37c画出了LC支路和电源L_s支路的谐波电流特性曲线。图中纵坐标为LC支路的谐波电流I_Cn、L_s支路谐波电流I_sn与负荷谐波电流I_n的比值（即分流系数K_Cn=I_Cn/I_n、K_sn=I_sn/I_n）。图中横坐标为谐波频率ω_n与L、C谐振频率的比值ω_n/ω_r，n为谐波阶次，ω₁为基波频率，横坐标为

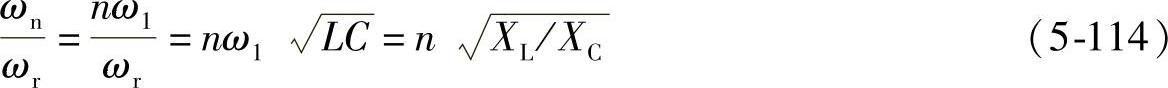
由式（5-108）～式（5-113）及图5-37c可清楚地看到：

1）图5-37c中在ω_n/ω_r=1的B点，nX_L=X_C/n，L、C支路串联电抗X_LCn=0，LC支路电流I_Cn=I_n，K_Cn=I_Cn/I_n=1，LC支路分流负荷的全部n次谐波电流，节点n次谐波电压V_n=0，线路电流I_sn=0、K_sn=I_sn/I_n=0，电源线路中不存在n次谐波电流。对于图5-37c中串联谐振点B有(www.xing528.com)

2）当ω_n/ω_r>1，即ω_n>ω_r，nX_L>X_C/n，L时，LC支路串联电抗为感抗XLCn>0，LC支路与L_s支路并联电抗为感抗，这时0<I_Cn<I_n，I_sn=I_n-I_Cn，0<I_sn<I_n，例如在图5-37c中的A点，LC滤波支路不能滤除I_n，但I_Cn、I_sn都小于I_n，不会发生谐波电流被放大的情况。

3）当ω_n/ω_r<1，即ω_n<ω_r、nX_L<X_C/n、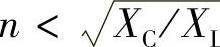L时，LC支路串联电抗X_LCn<0，X_LCn为容抗，但L_s支路仍为感抗，因此在同一个节点电压V_n作用下I_sn与I_Cn方向相反，但两者之和I_sn+I_Cn=I_n。从B点开始随着ω_n/ω_r的减小，I_Cn从I_n逐渐变大，K_Cn从1逐渐增大，而K_sn从0变负，负值越来越大，即电源L_s支路的谐波电流-I_sn越来越大。如果横坐标点从ω_n/ω_r=1的B点减小到C点时，I_Cn从I_n增大到I_Cn=2I_n，I_sn从零变为-I_n，由式（5-110）得到

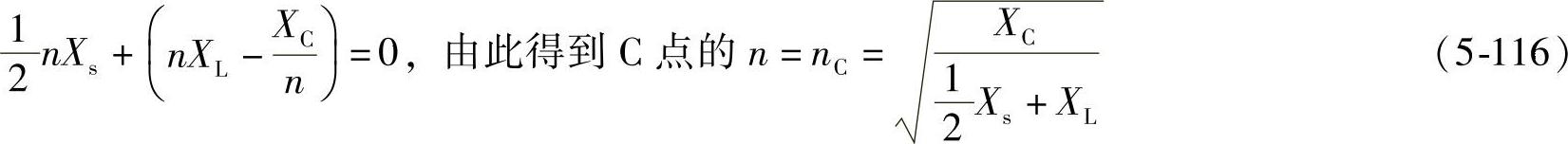
C点的横坐标值为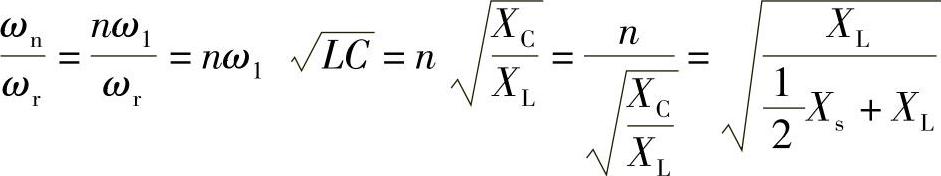

即在图5-37c中的C点，I_sn=-I_n，I_Cn=I_n-I_sn=2I_n。

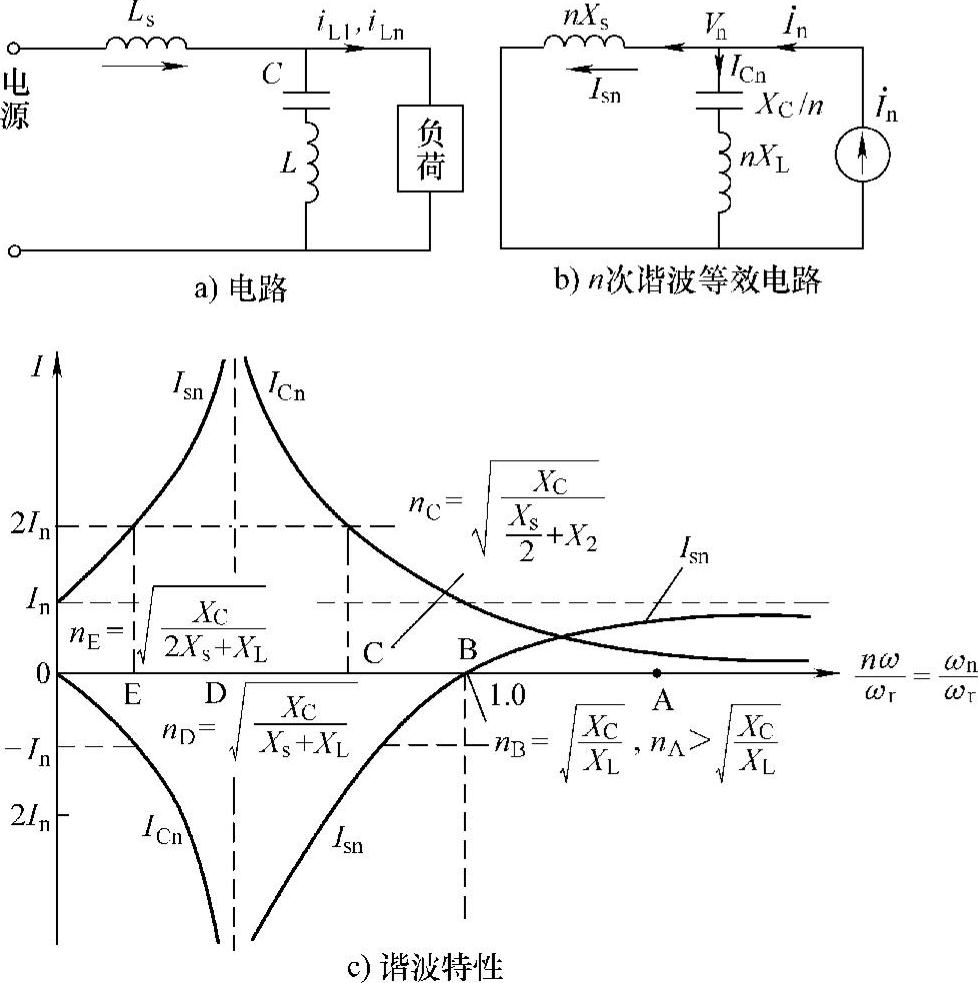
图5-37 R=0，考虑电源线路电感L_s时的谐波特性

4）当ω_n/ω_r从图5-37c中的C点继续减小时，I_sn的负值更大，即|I_sn|>I_n，I_Cn>2I_n。当ω_n/ω_r=nω₁/ω_r减小到LC支路的容抗等于L_s支路的感抗nX_s时，LC支路与L_s支路发生并联谐振，这时L_C与L_s的并联电抗趋近于无限大，负荷谐波电流I_n使电压V_n趋于正无限大，使I_Cn趋于无限大，I_sn趋于负无限大，如图5-37c中的D点。令式（5-108）中的L_C支路电抗X_LCn为容抗并等于L_s支路的感抗nX_s，可得到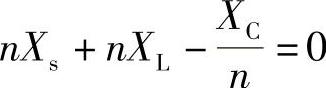，D点谐波频率的倍数为

在图5-37c中的CD区间I_sn从-I_n增大，I_Cn从2I_n增大。

5）当ω_n/ω_r从D点进一步减小时，LC支路的容抗大于L_s支路的感抗nX_s，这时式（5_-109）的分母变负，因此I_Cn从正值变为负值（与I_n反相），如果到E点I_Cn=-I_n，由式（5-109）得到E点的谐波频率倍数为

这时的I_sn由式（5-110）得到：I_sn=I_n-I_Cn=2I_n，即电源L_s支路的谐波电流I_Cn比负荷谐波电流I_n大一倍。

6）当ω_n/ω_r从E点趋于零时，由式（5-109）、式（5-110）可知，I_sn趋于I_n，I_Cn趋于零。由图5-37c可以清晰地看到，当谐波频率ω_n与LC谐振频率ω_r的比值，即ω_n/ω_r>1，ω_n>ω_r，nX_L>X_C/n，LC为感抗时，谐波相对频率n=ω_n/ω₁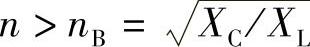，，LC滤波电路对阶次n大于n_B的谐波不会发生谐波放大，但谐波频率ω_n越高电源L_s支路分配的谐波电流比例越大，I_sn越大。

综上所述，当谐波阶次在BC区间时，有n_C<n<n_B，I_Cn>I_n，|-I_sn|<I_n；当谐波阶次在CD区间时，有n_D<n<n_C，I_Cn>2I_n，|-I_sn|>I_n；当谐波阶次在DE区间时，有n_E<n<n_D，|-I_Cn|>I_n，I_sn>2I_n；当谐波阶次在EO区间时，有0<n<n_E，|-I_Cn|<I_n，I_sn从2I_n→I_n。

以上分析结果对LC滤波器L、C参数值的正确选择有指导意义。例如，如果负荷最低次特征谐波电流为5次谐波（n=5），则LC的乘积应使其谐振频率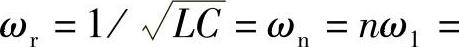5ω₁。此外，应根据LC滤波电路对基波无功补偿的要求，系统线路等值电感值L_s、电力系统不同运行工况时系统中的静止无功补偿器SVC的等效电抗、电容参数以及这些参数和LC滤波器自身参数发生变化范围，审查或校核系统可能发生的谐波电流放大的可能性。

2.高通滤波器

电网中高次谐波含量较低，同时由于高次谐波遇到的系统谐波阻抗大，因此滤除高次谐波不采用调谐滤波器。为了降低成本，通常采用一个高通滤波器将某一频率以上的高次谐波滤除。高通滤波器有二阶减幅型、三阶减幅型和C型三种，如图5-38所示。

L₁、C₁二阶高通滤波器的基波损耗不大，滤波性能好，结构简单，因此工程上应用最为广泛；C₁、L₁、C₂三阶高通滤波器的基波损耗很小，但特性不如二阶高通滤波器，因此用得不多；C型高通滤波器的性能介于二阶和三阶之间，C₂和L调谐在基波频率上，使基波电流不通过电阻，因此可以大大降低基波损耗。C型高通滤波器在工程上也较常用，其缺点是长工作时间后，电容、电感参数变化导致调谐频率偏移基波，基波损耗将明显增大。

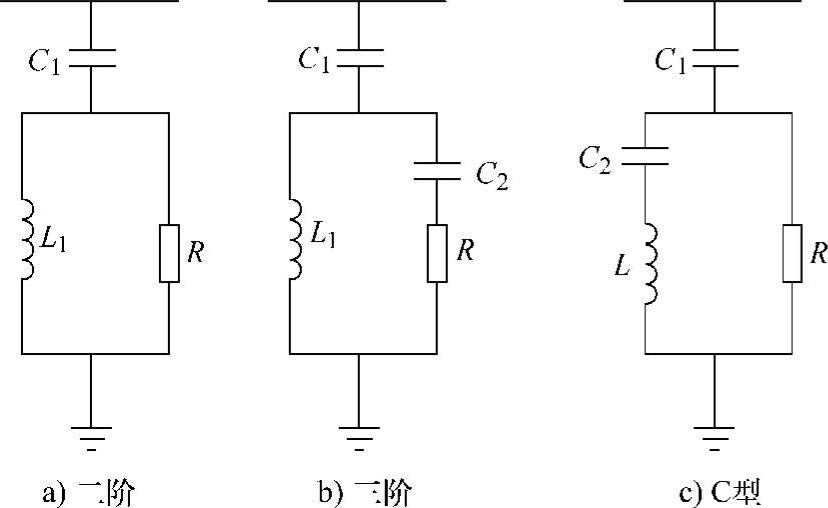
图5-38 各种型式的高通滤波器

在工程中设计无源滤波器时，应详细了解负荷各种工作情况下（稳态与动态）谐波电流的频率成分，这是选择单调谐滤波器及高通滤波器的依据。此外，还应详细了解电网的阻抗特性，从而可以分析出所选用的滤波器的滤波效果（谐波分流效果），并防止出现谐振放大谐波电流；还应充分考虑LC滤波器的基波特性（无功补偿功率），不要造成谐波满足要求而无功特性不满足要求。最后，还应注意，监控长时间运行后电感、电容参数的变化。