受电力电子开关器件额定电压、电流的限制，电力系统中所有的高压大容量静止无功同步补偿器STATCOM都只能由多个单相桥或三相桥“单元”组合而成。这种组合系统中的单相桥或三相桥“单元”其输出电压的幅值和相位都是可控的，即使每个单元只输出一个脉宽为θ的单脉波（这时开关频率很低，变流器开关损耗小）。只要适当地安排各变流单元输出电压波形的脉宽θ和相位差，就有可能使整个变流系统输出电压中的基波电压幅值，且相位可控。同时，还可消除一些低次谐波，削弱某些高次谐波。而高次谐波又易于用LC无源滤波器抑制，因此在变流系统中对开关器件仅采用较低的开关频率下也能使总的输出电压为幅值和相位可控的近似正弦波，可以把这种大容量变流系统作为可控的电压源，研究其运行特性和控制特性。如果要研究其谐波特性也可用叠加法，单独对谐波特性进行研究。下面将研究图5-22a所示由三个相差120°、输出电压等效脉宽为θ的单相电压源变流器所组成的三相STATCOM，图中交流电压V1A、V1B、V1C经线路电抗XL对负载供电。在图5-22b中，若STATCOM变流器运行时变流器开关器件的全部功耗为PSVG，忽略变流器输出端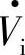
与电网电压
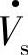之间很小的电阻（即取R=0），变流器交流输出电压
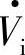经电抗X=ωL接电网电压Vs，变流器向系统输出电流I。如果三相变流器直流侧电压为VD，STATCOM交流侧输出电压ViA、ViB、ViC均为幅值为脉宽θ的单脉波，如图5-22c或图5-25b所示的方波EKPB，其基波ViA1的幅值为Vim。图5-23b所示变流器交流输出端输出电压
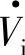比电网负载端电压
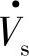滞后δ，若电网A相电压vsA=Vsmcosωt，则变流器输出的A相基波电压为
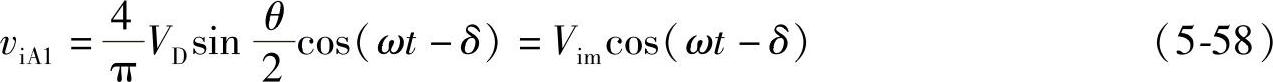
式中，Vim是三相变流器输出交流相电压幅值，它是直流电压VD和脉宽θ的函数，即
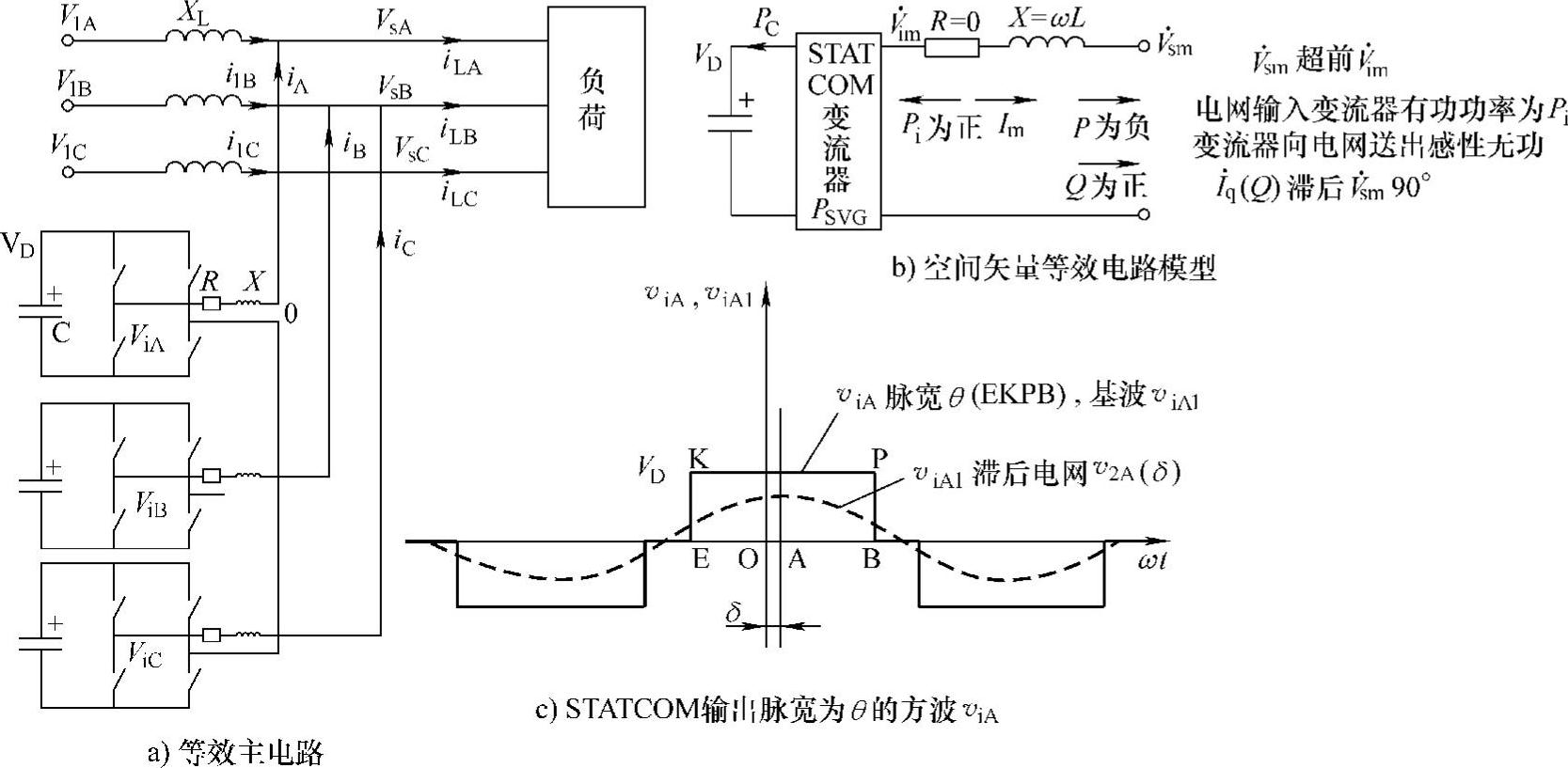
图5-22 STATCOM电路
直流电压VD变为交流电压Vim的变流系数为
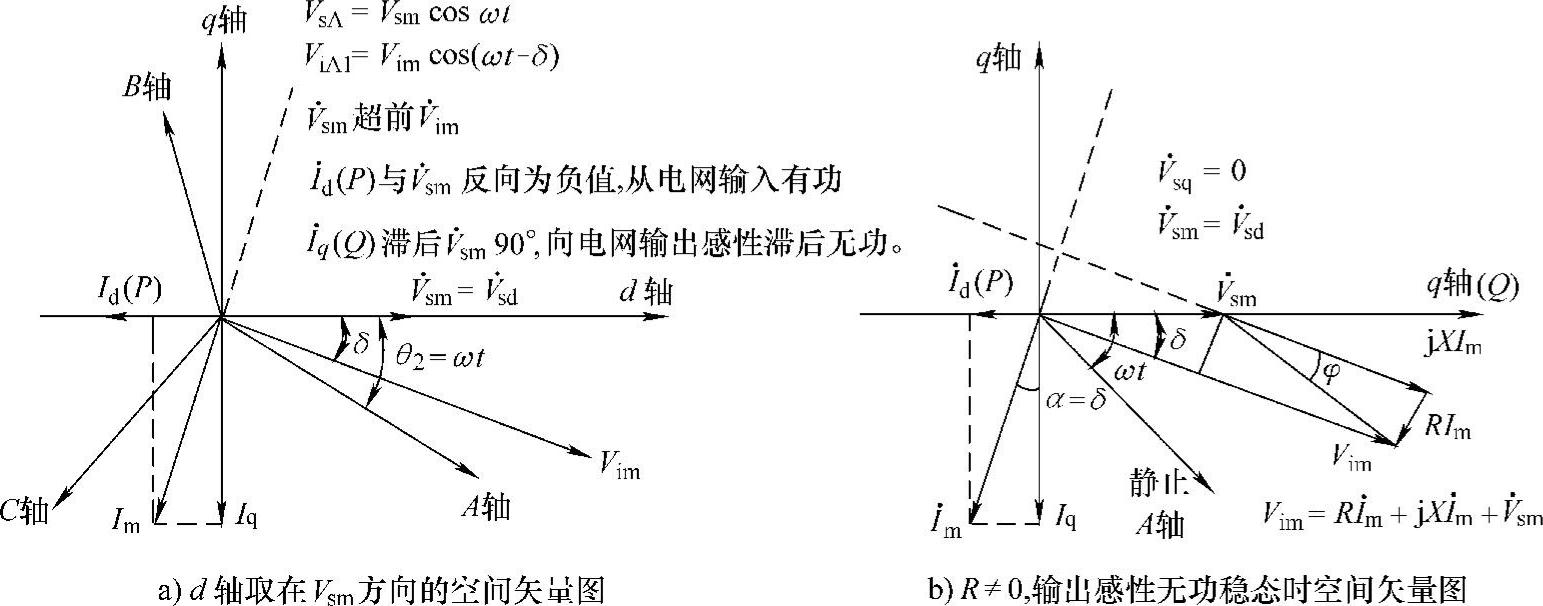
图5-23 STATCOM等效电路空间矢量
由式（2-84A），在A、B、C三相静止和d、q两相旋转坐标系中变流器（电压Vim）输出的三相有功功率为
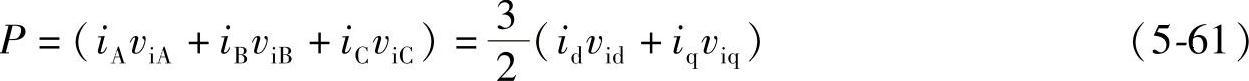
图5-23中选取d、q坐标的d轴在电网电压空间矢量Vsm的方向，则电网电压在d、q坐标系中的空间矢量Vsm在d轴分量为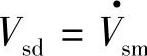
；q轴分量Vsq=0。变流器输出电压空间矢量
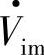滞后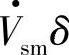
，
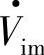的d、q分量为Vid=Vimcosδ、Viq=-Vimsinδ。由式（5-59）可得
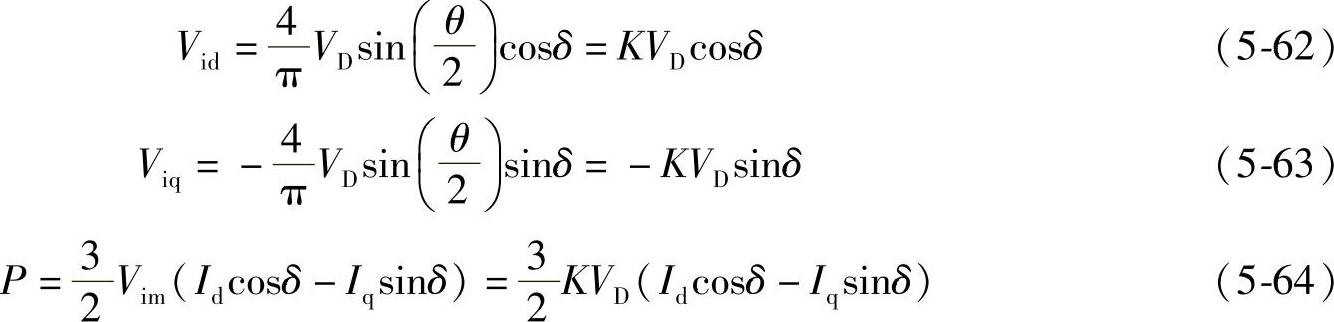
图5-24a是将变流器的功耗PSVG纳入STATCOM内部的等效电路模型、STATCOM运行中的功耗由两部分构成：①开关器件在开通和关断过程中的开关损耗，其值正比于电压、电流的乘积；②开关器件的通态电压降损耗，其值正比于电流。图5-24b中STATCOM与电网电压Vsm正交的无功电流Iq远大于有功电流Id，电流Im≈Iq（若Iq=1.0，Id=0.1，则Im=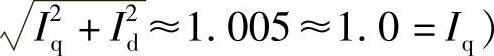
，因此STATCOM运行时变流器的功耗PSVG可以表达为
PSVG≈K1VD|Iq|+K2|Iq| （5-65）
式中，|Iq|为Iq的绝对值；K1、K2分别为开关损耗和通态损耗比例系数。电压为VD时电容C的储能WC=CV2D/2。C充电时VD上升，充电功率为PC，即
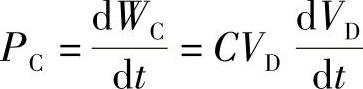
由图5-24a，PSVG与PC之和应与电网输入变流器的功率Pi平衡，Pi=PC+PSVG=-P，即
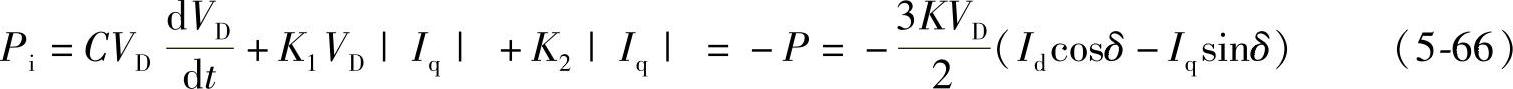
由此可以得到
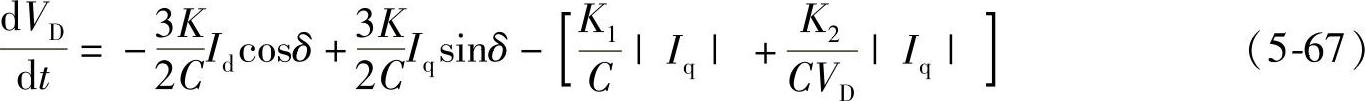
类似于式（2-63）、式（2-64），图5-24中d、q坐标系电压平衡方程为
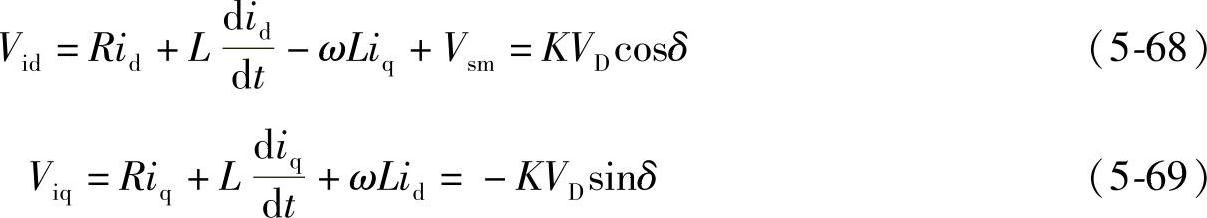
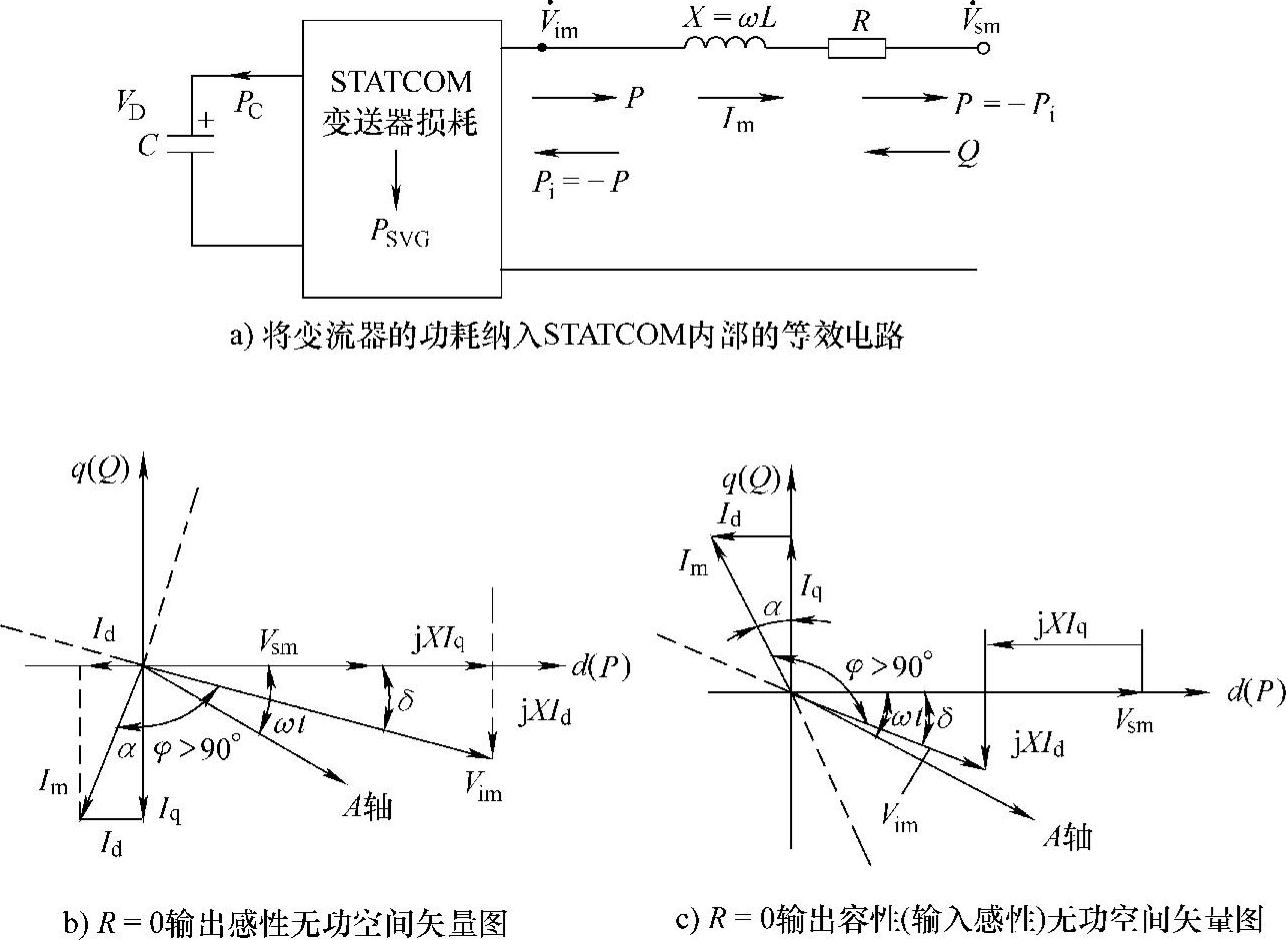
图5-24 采用内部功耗模型的STATCOM模型电路和空间矢量图
以上两式中的电阻R、X=ωL是变流器输出端与电网电压VS之间的电阻、电抗。由式（5-67）、式（5-68）、式（5-69）可以得到状态方程为
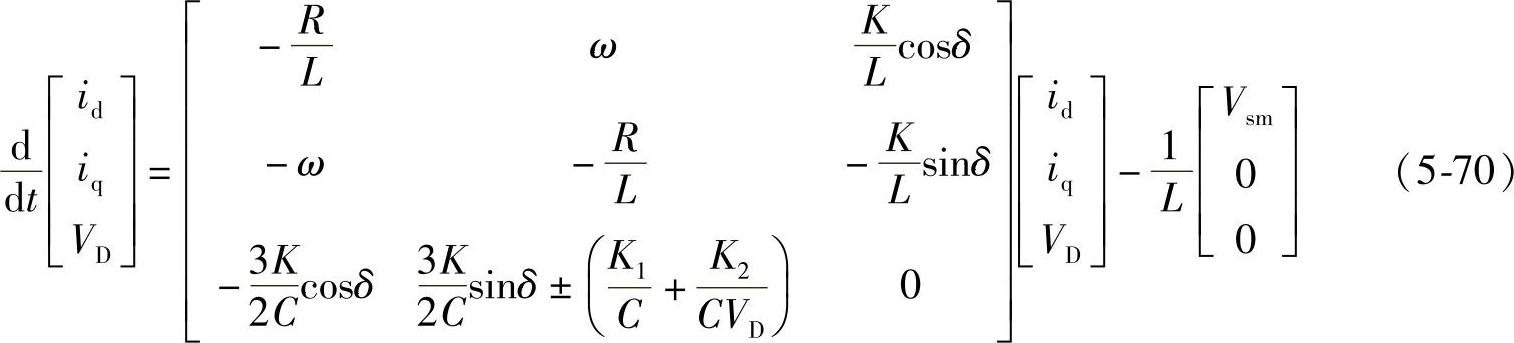
式中，K=Vim/VD。
由于式（5-67）中功率损耗所对应的电流Iq只能取绝对值，因此式（5-70）中的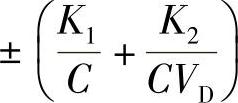
项，当iq为负值时取正号，iq为正值时取负号。式（5-70）是基于图5-24的STATCOM等效电路所得到的d、q系统状态方程，依此可分析研究STATCOM的动态特性。在式（5-70）中，令R=0，即为忽略输出电路电阻时的状态方程。稳态运行时VD、id、iq为定值，STATCOM输出给电网的有功电流为
输出给电网的感性（滞后）无功电流为(www.xing528.com)
电网输入到变流器的三相有功功率为
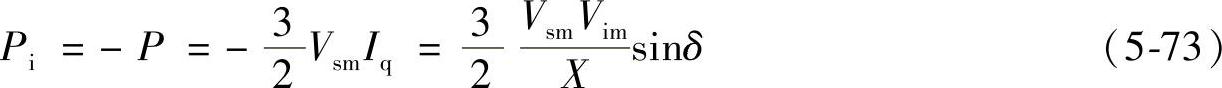
输出至电网的感性（滞后）无功功率为
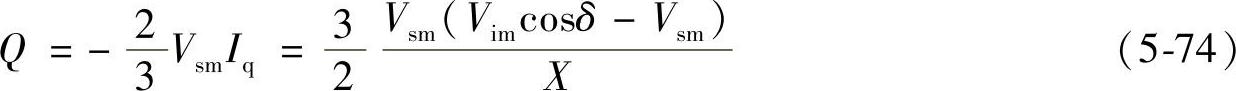
STATCOM运行中有功电流Id远小于无功电流Iq，图5-24b中若Vsm=1.0，即使Id=0.5Iq，若无功电流电抗电压降XIq=0.1，XId=0.05，则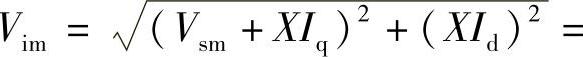
1.101，而Vsm+XIq=1.1，Vsm与Vim（1.101）相差仅0.1%，这时cosδ=0.999，δ=2.6°（δ=2.6°=2.6×π/180°=0.0454，sinδ=0.04537，用弧度表示的δ与sinδ相差远小于0.1%），Vimcosδ=1.101×0.999=1.0999≈1.1≈Vim，因此由式（5-72）、式（5-74）式得到
由（5-74）式可以得到
由式（5-75）和式（5-60）可得直流电容电压为
电网输入到STATCOM的三相有功功率Pi应等于式（5-65）的变流器功耗PSVG，由式（5-65）、式（5-75）及式（5-60）的VD=Vim/K，可得到
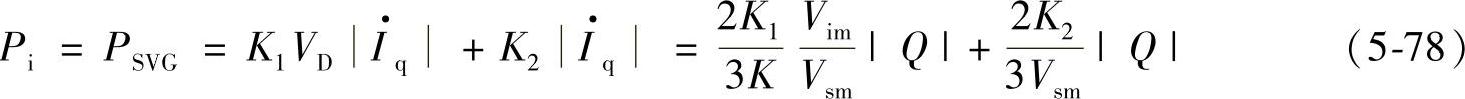
由以上两式得到
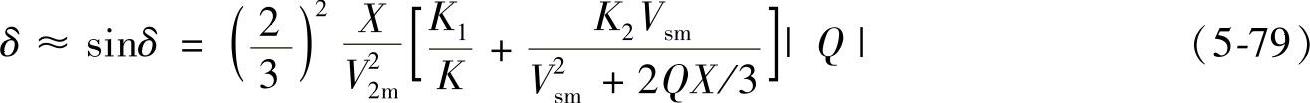
式中，STATCOM向电网输出感性无功时Q取正值。
请留意以上各式中的电压、电流都是d、q坐标系中空间电压、电流矢量的幅值。
当要求STATCOM输出的无功功率为指令值Q∗时，由式（5-76）和式（5-77）可确定指令值θ∗所需的Vim、VD。在VD下稳定运行所需电网输入的有功功率由式（5-78）确定，对应的功率角δ由式（5-79）确定，δ是变流器输出电压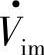
滞后电网电压
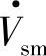的相位角。研究STAT-COM运行特性采用图5-24a所示模型，要比有些文献中将变流器内部全部功耗PSVG用外电路一个等效电阻R来模拟更为合理。同时，式（5-65）中代表变流器功耗的系数K1、K2的取值，要比将变流器中的全部功耗等效电阻R的取值要简便、可行，且较符合实际，也更精确。按图5-24a模型及由此得到的各变量Vim、VD、P、δ与无功指令Q的函数关系式也更清晰合理，无论是分析计算STATCOM运行特性还是构建控制系统都较合适。
STATCOM输出脉宽θ的单脉波时，直流-交流电压变换系数K=Vim/VD=4sin（θ/2）/π，Vim=KVD。如果STATCOM的输出电压不是单脉波，则输出电压基波幅值Vim仍可表达为Vim1=MVD，这时上式中直流电压VD变为交流基波电压Vim1的变压比M与变流器开关管的控制策略有关。例如，如果每个单相桥变流器采用正弦脉冲宽度调制SPWM控制时，变压比M被称为调制比，它是正弦参考波电压幅值Vrm与高频三角载波幅值Vcm的比值。
M=Vrm/Vcm （5-80）
Vim=MVD=VDVrm/Vcm （5-81）
这时，如图5-24b、c所示，取d轴在电网电压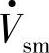
方向上，
，
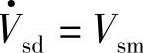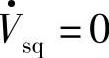，有
Vid=Vimcosδ=MVDcosδ
Viq=Vimcos（δ+90°）=-Vimsinδ=-MVDsinδ（5-82）
这时，d、q系统中STATCOM变流器的数学模型只需将式（5-70）中的K换为M即可，即
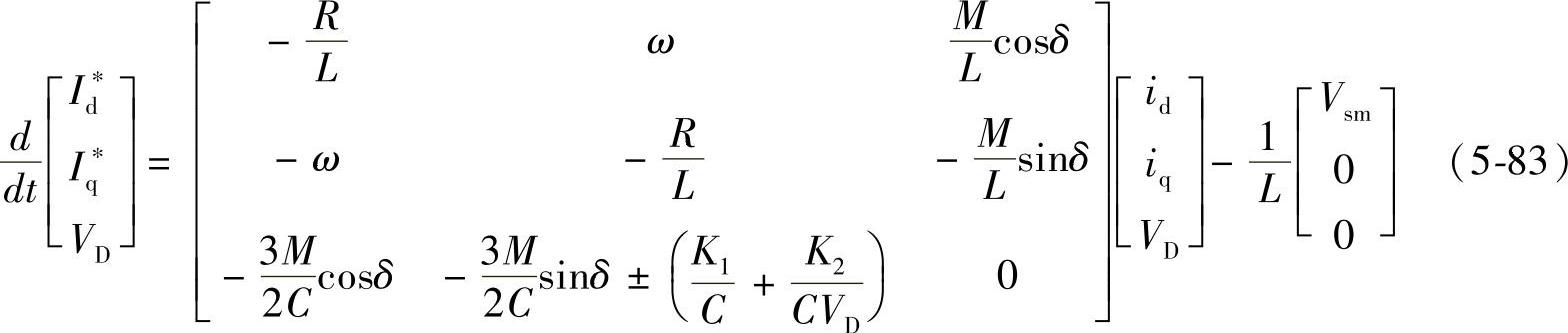
三相桥变流器电路，是实现直流、交流变换最基本、最重要的电力电子变换电路。为了研究电路的运行特性，特别是暂态时电压、电流、功率等运行参数的控制特性，如果直接求解A、B、C坐标系的三相电压平衡方程有诸多不便。引入d、q坐标系变量后，A、B、C三相耦合的电压、电流，变为正交的两相电压、电流，基波变为直流，n次谐波变为n-1次谐波电压、电流。在d、q坐标系电压、电流方程中，很容易从电流、电压中分离出基波和谐波，有利于对系统运行特性，特别是对系统暂态特性的分析计算。此外，在d、q坐标系中还有可能简化控制系统结构，易于引入新的控制策略，增加对系统运行特性的调控功能和改善系统运行的控制特性，更易于实现给定控制目标的最优控制。
本节最后再说明一下STATCOM输出脉宽为θ的单脉波时，开关器件的驱动触发开通角如何确定。图5-25a示出了基波电压等效电路和空间矢量图，在图5-25b中由STATCOM输出脉宽为θ的单脉波电压（方波EKPB）ViA、ViA的基波为ViA1，基波电压ViA1的幅值为Vim，Vsm为电网电压，X为STATCOM输出端与电网节点之间的等效电抗。图5-25b中画出了STATCOM A相输出脉宽为θ的单脉波电压ViA、其基波ViA1和电网A相电网电压
的波形。STATCOM输出基波电压ViA1滞后电网电压VsA相位角为δ，图中时间坐标零点取在VsA的最大值处。输出端方波电压ViA的起点为E，脉宽为θ的方波ViA的中点为A，EA=AB=θ/2。viA的基波ViA1的零点D超前脉宽θ的起点E的相位角β=DE=DA-EA=90°-θ/2，电网电压VSA的零点F超前ViA1的起点D相位为δ，因此VsA零点F超前脉宽为θ的方波的起点E的相位角FE=FD+DE=δ+β=90°+δ-θ/2，即脉波θ的起点E滞后电网电压VsA的零点F相位角为αp=FE=δ+β=90°+δ-θ/2。所以检测到电网电压VSA过零点F后，延时一个相位角αp=δ+β=90°+δ-θ/2，应触发开通STATCOM中A相变流器的开关管S1、S4，使ViA=VD，S1、S4导通θ后，在图5-25b中的B点应关断A相上开关管S1，开通S2、S4，使ViA=0（关断点B对应的ωt=OB=δ+θ/2），使变流器输出脉宽为θ的方波EKPB。
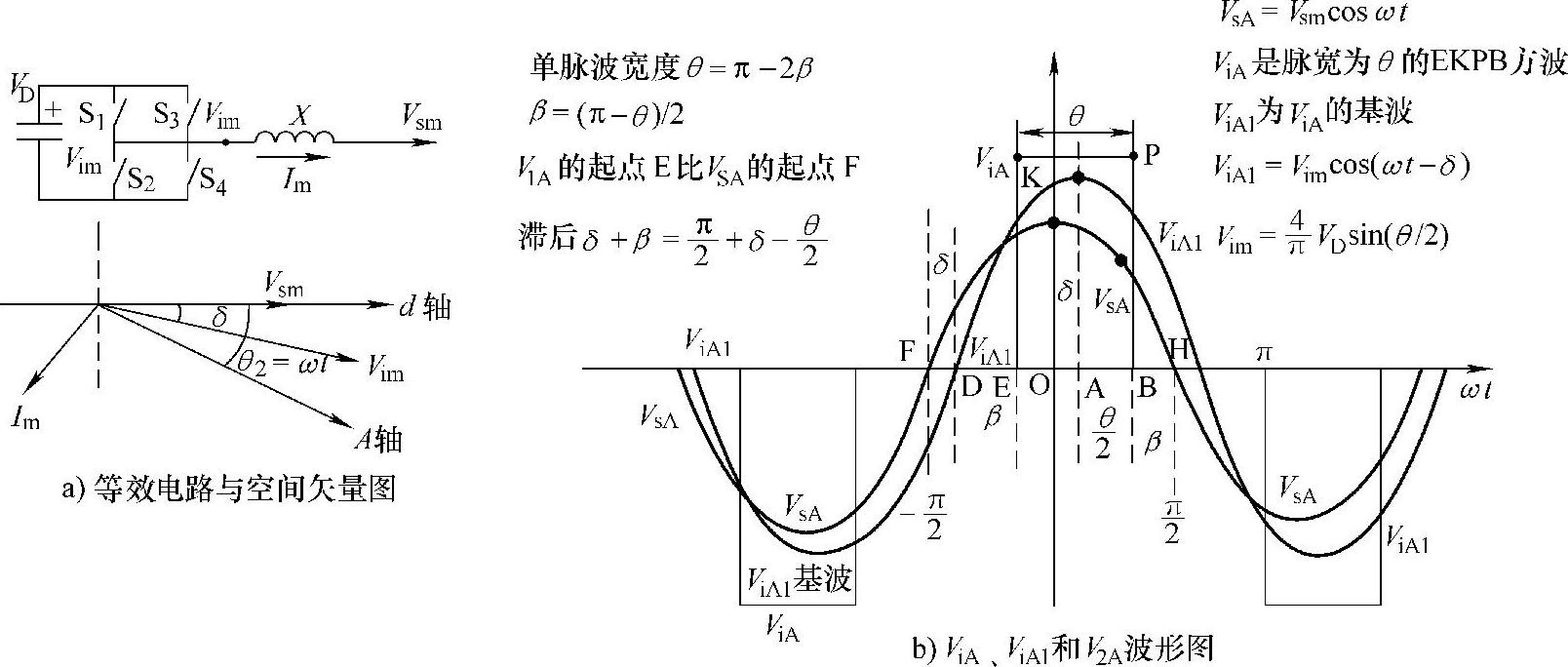
图5-25 说明开关器件驱动信号的电压矢量图及波形图
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
