直流输电系统等效电路剖析

图4-10a和图4-10b为直流输电首端相控整流电路及相控整流相量图。α₁<90°，V_d1>0，即P₁（A）点为正，N₁（B）点为负，交流电源电压V₁输入三相整流桥的电流为I·₁，换流重叠角为γ₁，功率因数角为φ₁，则整流电路输出的整流电压V_d1、有功功率P_r和无功滞后功率Q_r分别为

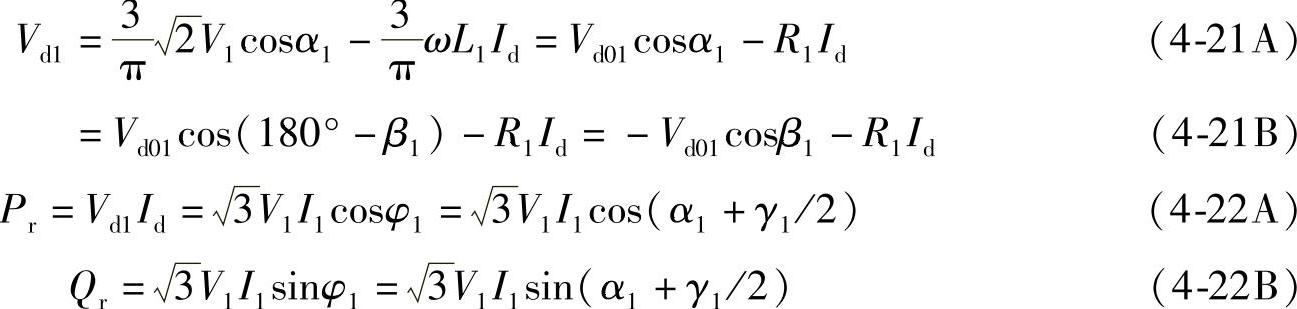
式中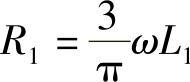，是送端换流器换相电压降等效电阻；V_d01是α₁=0时空负荷电压。

直流输电功率为P_DC=P_r，功率因数角为

φ₁=α₁+γ₁/2 （4-23）

线路送端换流器考虑换流重叠过程时的直流电流I_d，由式（2-19）可得

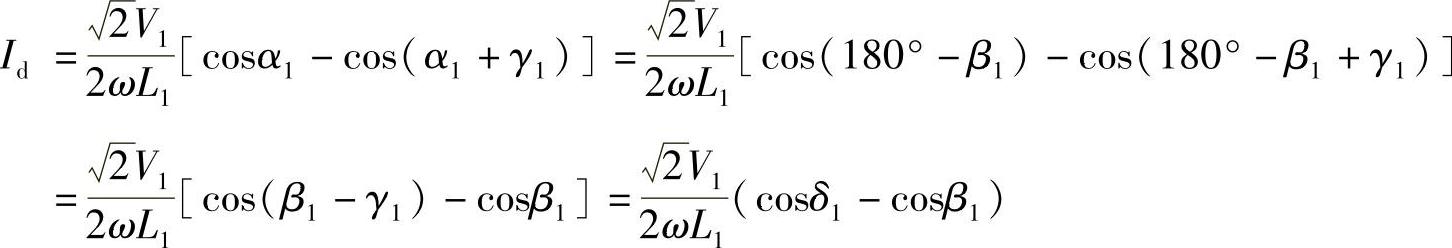
式中，β₁为逆变角，β₁=180°-α₁；γ₁为换相重叠角；关断角δ₁=β₁-γ₁。

由此得到：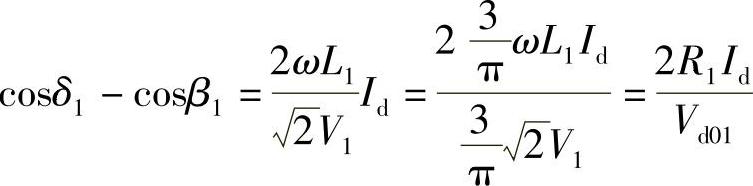

V_d01 cosδ₁-V_d01 cosβ₁=2R₁I_d （4-24A）

由上式，式（4-21B）可改写为

V_d1=2R₁I_d-V_d01 cosδ₁-R₁I_d=R₁Id-V_d01 cosδ₁ （4-21C）

逆变电压为

图4-10 直流输电系统电路、相量图和等效电路

V_i1=-V_d1=V_d01 cosδ₁-R₁I_d （4-25）

因此，在图4-10中，V_d1可用式（4-21A）、式（4-21B）或式（4-21C）的α₁、β₁或δ₁函数关系表达。式（4-24A）是β₁、δ₁和换相电压降的关系式。

图4-10c和图4-10d分别为直流输电受端相控有源逆变电路及相量图，这时触发延迟角α₂>90°，α₂=180°-β₂，β₂为逆变角。若换流重叠角为γ₂，关断角δ₂=β₂-γ₂，则三相逆变桥直流端输出电压V_d2=V_P2N2<0，即图4-10c中N₂（C）点为正，P₂（D）点为负。负值整流电压-V_d2被称为逆变电压V_i2，则V_i2=-V_d2=-V_P2N2=V_N2P2。图4-10c中若令交流电源电压送入三相逆变桥的电流为I·₂，则有源逆变电路直流侧整流电压V_d2，逆变电压V_i2（V_i2=-V_d2）以及交流电源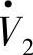送入三相逆变桥的有功功率P_i、无功功率Q_i分别为

式中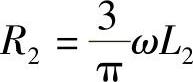，是受端换流器换相电压降等效电阻；是α₂=0°时整流空载电压。

类似于式（2-19），对受端换流器有

由此式得知：

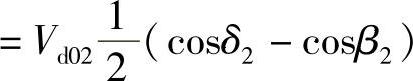（关断角δ₂=β₂-γ₂）(www.xing528.com)

故有

式中，交流电流基波有效值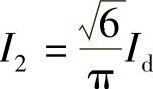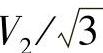，；是交流相电压有效值；ωL₂I₂是换相电抗ωL₂引起的交流电压降，换相交流压降的相对值ΔV_L∗₂=ωL₂I₂/V₂/3，通常额定交流电压、电流时的ΔV_L∗₂约为5%（0.05），故

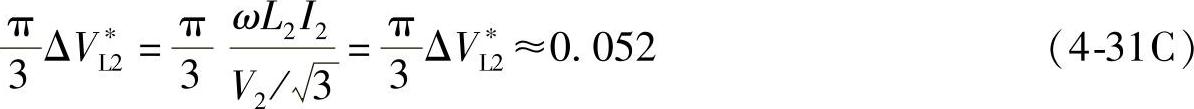
由式（4-31A）可得换流重叠角为

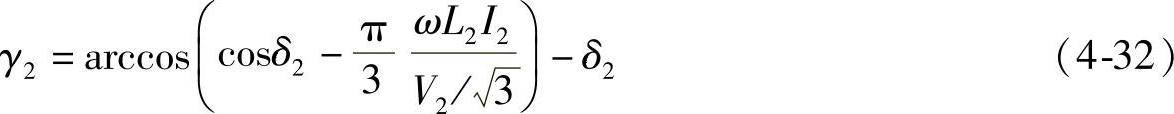
由式（4-31A）也可得到关断角为

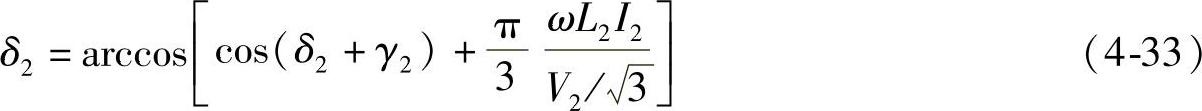
由式（4-31B）也可得到相控触发延迟角

将式（4-24B）代入式（4-27B）可得到

V_i2=-V_d2=V_d02 cosδ₂-2R₂I_d+R₂I_d=V_d02 cosδ₂-R₂I_d （4-27C）

相控有源逆变器的滞后无功功率为

图4-10f和图4-10g分别示出用相控逆变器的逆变角β₂（β₂=180°-α₂）和关断角δ₂表达的等效电路。关断角δ₂=β₂-γ₂=180°-α₂-γ₂，请注意图4-10f和图4-10g中的有源逆变换相重叠等效电压降的等效电阻分别为R₂和负值-R₂。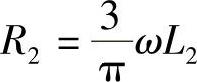与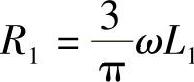一样，都是换流重叠电压降的等效虚拟“电阻”，并不产生功耗。读者还应注意逆变运行时的关断角的物理意义：某个晶闸管如VT₁被触发开通后，其电流i_VT1在γ期间逐渐从零上升至I_d，原来处于导通的晶闸管VT₅电流i_VT5（i_VT5=I_d-i_VT1）在VT₅、VT₁同时导通电流的换流重叠γ期间从I_d下降为零（关断），换流结束。若换流结束VT₅断流后，VT₅在电路中仍有一段时间t_δ使已关断的晶闸管VT₅仍承受反压阻止其再导通，逆变工况运行时反压时间t_δ所对应的角度δ=ωt_δ就被称为关断角（参见图2-13相关说明）。关断角δ=180°-α-γ=β-γ。晶闸管断流后，其内部导电载流子需经过一段恢复时间t_off才能复合消失，经恢复时间后才能具有阻断能力，阻断外加正向电压时再次误导通。因此实际逆变工况的运行中，t_δ=δ/ω>t_off=δ_off/ω，即逆变运行时，关断角δ必须大于t_off对应的相位角δ_off，即必须δ>δ_off。

若输电线电阻为R_L，则由等效电路图4-10f得：

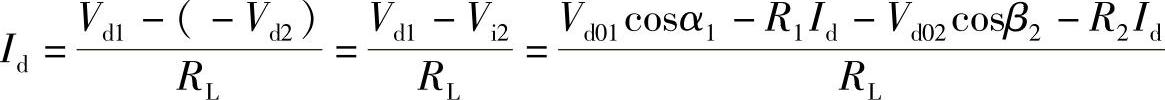
得到： （4-35）

或 （4-36）

由等效电路图4-10g及式（4-27C）的-V_d2可得

式（4-35）和式（4-37）分别是由逆变角β₂和关断角δ₂所确定的直流电流表达式。如果交流电流为120°脉宽的方波，则或交流电流基波有效值。式（4-21）、式（4-27）和式（4-35）、式（4-36）、式（4-37）及图4-10b、d、f和g可方便地用于分析研究直流输电系统特性和控制策略。

再次强调，半控型开关器件晶闸管相控整流和有源逆变实现有功功率变换的同时必须由交流系统提供滞后的（感性）无功功率；图4-10c中的I·₂是交流电源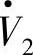送入三相有源逆变桥的电流。式（4-28）的P_i是交流电源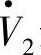送入三相逆变桥的有功功率，P_i为负值，表明这个有功功率是从三相逆变桥流出到交流电压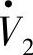，即逆变桥实现将直流侧有功功率变换为交流有功功率，送入交流电压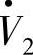的电力系统；相控整流时的功率因数角为φ₁=α₁+γ₁/2；有源逆变时的功率因数角φ₂为α₂+γ₂/2或β₂-γ₂/2，β₂=180°-α₂=γ₂+δ₂。